回答
https://math.pro/db/viewthread.php?tid=1569&page=4#pid9314 insel的疑問
既然寸絲將這單元取名為"Fubini定理",那妳就要先知道什麼是Fubini定理。
請參考游森棚老師所寫的文章
連結已失效h ttp://highscope.ch.ntu.edu.tw/wordpress/?p=14687
107.9.9補充
在2013年在科學月刊發表的"算兩次"文章,內容大同小異
連結已失效h ttp://scimonth.blogspot.tw/2013/12/blog-post_5.html
整篇最重要的觀念就是
用兩個方法算同一個量, 結果會一樣
回到寸絲筆記math note 01-10第2.6單元 富比尼定理
求:\( \displaystyle 1 \times (1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{99}+\frac{1}{100})+3 \times (\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots +\frac{1}{99}+\frac{1}{100}) \)
\( \displaystyle +5 \times (\frac{1}{3}+\frac{1}{4}+\ldots \frac{1}{99}+\frac{1}{100})+\ldots+197 \times (\frac{1}{99}+\frac{1}{100})+199 \times \frac{1}{100} \)
(100麗山高中2招,
https://math.pro/db/thread-1164-1-1.html)
[解答]
原本題目是橫的總和,改算直的總和,結果當然一樣
\( \matrix{1 & \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& \frac{1}{2} & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & \frac{1}{3} & \ldots & \frac{1}{99} & \frac{1}{100} \cr
& & & \ldots & & \cr
& & & & \frac{1}{99} & \frac{1}{100} \cr
& & & & & \frac{1}{100}} \)
-----------------
\( \displaystyle 1 \times 1+4 \times \frac{1}{2}+9 \times \frac{1}{3}+ \ldots +99^2 \times \frac{1}{99}+100^2 \times \frac{1}{100}=5050 \)
111.2.14補充
計算\(\displaystyle 1\times(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5})+3\times(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5})+5\times(\frac{1}{3}+\frac{1}{4}+\frac{1}{5})+7\times(\frac{1}{4}+\frac{1}{5})+9\times \frac{1}{5}=\)?
(A)13 (B)14 (C)15 (D)16
(106台北市國中聯招)
103.9.6補充
若\( log_5 144^{\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{10}}+2 log_5 144^{\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{10}}+3 log_5 144^{\frac{1}{4}+\frac{1}{5}+\ldots+\frac{1}{10}}+\ldots+9 log_5 144^{\frac{1}{10}}=a log_5 2+b log_5 3 \),則\( a+b= \)?
(103新化高中,
https://math.pro/db/thread-2022-1-1.html)
(105桃園高中,
https://math.pro/db/thread-2489-1-1.html)
[提示]
\( \displaystyle 1(\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{10})+2(\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{10})+3(\frac{1}{4}+\frac{1}{5}+\ldots+\frac{1}{10})+\ldots+9(\frac{1}{10}) \)
\( \displaystyle =(1)\frac{1}{2}+(1+2)\frac{1}{3}+(1+2+3)\frac{1}{4}+\ldots+(1+2+\ldots+9)\frac{1}{10} \)
105.5.6補充
計算\( \displaystyle \left( \frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{2006} \right)+\left( \frac{2}{3}+\frac{2}{4}+\ldots+\frac{2}{2006} \right)+\left( \frac{3}{4}+\ldots+\frac{3}{2006} \right)+\ldots+\left( \frac{2004}{2005}+\ldots+\frac{2004}{2006} \right)+\frac{2005}{2006} \)
(2006青少年數學國際城市邀請賽 個人賽)
105.5.6補充
計算\( \displaystyle \frac{1}{1}+\left( \frac{2}{1}-\frac{1}{2} \right)+\left( \frac{3}{1}-\frac{2}{2}+\frac{1}{3} \right)+\left( \frac{4}{1}-\frac{3}{2}+\frac{2}{3}-\frac{1}{4} \right)+\ldots+\left( \frac{9}{1}-\frac{8}{2}+\frac{7}{3}-\frac{6}{4}+\ldots+\frac{1}{9} \right) \)
(建中通訊解題 第96期,
http://web2.ck.tp.edu.tw/~mathwe ... 30-15&Itemid=37)
108.5.18補充
設\(a,b,c,d \in R,abcd \ne 0\),且\(a+b+c+d=0\),則
\(\displaystyle a(\frac{1}{b}+\frac{1}{c}+\frac{1}{d})+b(\frac{1}{c}+\frac{1}{d}+\frac{1}{a})+c(\frac{1}{d}+\frac{1}{a}+\frac{1}{b})+d(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})\)之值為
。
(108麗山高中,
https://math.pro/db/thread-2742-1-1.html)
[提示]
\(\matrix{\displaystyle &+&\frac{a}{b}&+&\frac{a}{c}&+&\frac{a}{d} \cr
\frac{b}{a}&+& &+&\frac{b}{c}&+&\frac{b}{d} \cr
\frac{c}{a}&+&\frac{c}{b}&+& &+&\frac{c}{d} \cr
\frac{d}{a}&+&\frac{d}{b}&+&\frac{d}{c}&+& \cr}\)
-----------------
\( y=[\; x ]\; \)表高斯函數,求\( \displaystyle\Large\sum_{k=1}^{40}\left[10^{\frac{k}{40}}\right] \)
(101文華高中,
https://math.pro/db/thread-1333-1-3.html)
[解答]
觀察函數\( y=10^{\frac{x}{40}} \)的圖形,要計算格子點的個數。

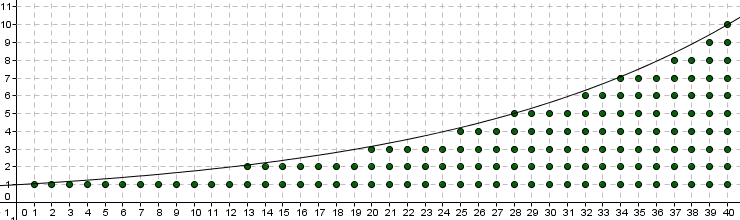
原本應該直著算(\( x=1 \)有1個點,\( x=2 \)有1個點,...,\( x=39 \)有9個點,\( x=40 \)有10個點)
改成橫著算,也就是\( \displaystyle \Large 10^{\frac{x}{40}}\ge j \),\( x \ge 40 \times log(j) \),會有幾個x值(當然\( x \le 40 \))
\( j=1 \),\( x \ge 40 log(1)=0 \),有40個點
\( j=2 \),\( x \ge 40 log(2)=12.0411 \),有28個點
\( j=3 \),\( x \ge 40 log(3)=19.0848 \),有21個點
\( j=4 \),\( x \ge 40 log(4)=24.0823 \),有16個點
\( j=5 \),\( x \ge 40 log(5)=27.9588 \),有13個點
\( j=6 \),\( x \ge 40 log(6)=31.1260 \),有9個點
\( j=7 \),\( x \ge 40 log(7)=33.8039 \),有7個點
\( j=8 \),\( x \ge 40 log(8)=36.1235 \),有4個點
\( j=9 \),\( x \ge 40 log(9)=38.1697 \),有2個點
\( j=10 \),\( x \ge 40 log(10)=40 \),有1個點
共141個格子點
\( \displaystyle \sum_{k=1}^{2013} \Bigg[\; \root 5 \of{\frac{2013}{k}} \Bigg]\; \)
(102建國中學,
https://math.pro/db/viewthread.php?tid=1569&page=1#pid7760)
[提示]

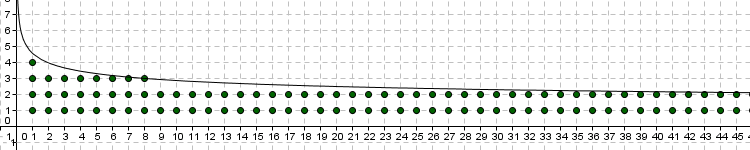
這就可以解釋為什麼寸絲要計算\( \displaystyle \Bigg[\; \root 5 \of{\frac{2013}{k}} \Bigg]\; \ge n \),\( \displaystyle \frac{2013}{k}\ge n^5 \),\( \displaystyle \frac{2013}{n^5}\ge k \ge 1 \)
\( n=1 \),\( \displaystyle \frac{2013}{1^5}\ge k \),有2013個點
\( n=2 \),\( \displaystyle \frac{2013}{2^5}\ge k \),有62個點
\( n=3 \),\( \displaystyle \frac{2013}{3^5}\ge k \),有8個點
\( n=4 \),\( \displaystyle \frac{2013}{4^5}\ge k \),有1個點
共2084個點
113.1.27補充
說明:本題中\([\;x ]\;\)為高斯符號,表示小於或等於x的最大整數,例如:\([\;\sqrt{2} ]\;=1\)、\([\;7 ]\;=7\)。
求\(1000~2022\)連續正整數的四次方根後再取高斯符號之總和
即求\([\;\root{4}\of {1000}]\;+[\;\root{4}\of {1001}]\;+[\;\root{4}\of {1002}]\;+\ldots+[\;\root{4}\of {2021}]\;+[\;\root{4}\of {2022}]\;\)的值為
。
(111台中一中科學班,
https://acad.tcfsh.tc.edu.tw/zh_tw/science/cos11)
我想寸絲應該是參考高中數學競賽教程第32講 福比尼原理 所以才用集合的寫法
而我是參考单壿老師所寫的書"算两次",在第3章 格點計算 有討論類似的問題,用的是幾何的方法
另外書上還有一些問題可以讓各位練習看看
1.設\( p,q \)為互質的自然數,證明\( \displaystyle \Bigg[\; \frac{p}{q} \Bigg]\;+\Bigg[\; \frac{2p}{q} \Bigg]\;+\ldots+\Bigg[\; \frac{(q-1)p}{q} \Bigg]\;=\frac{(p-1)(q-1)}{2} \)
2.設\( p,q \)為互質的自然數,證明\( \displaystyle \sum_{m=1}^{[1/2(q-1)]}\Bigg[\; \frac{mp}{q} \Bigg]\;+\sum_{n=1}^{[1/2(p-1)]}\Bigg[\; \frac{nq}{p} \Bigg]\;=\Bigg[\; \frac{p-1}{2} \Bigg]\; \times \Bigg[\; \frac{q-1}{2} \Bigg]\; \)
3.設n為自然數,證明\( \displaystyle [\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+\ldots+[\sqrt{n^2}]=\frac{1}{6}n(4n^2-3n+5) \)
--------------------------------
112.4.25補充
對集合\(\{\;1,2,\ldots,n \}\;\)的每一個非空子集定義"交錯和"如下:將該子集的元素依遞減次序排列,然後從最大的數開始交錯地減或加後繼的數(例如子集\(\{\;1,2,4,6,9 \}\;\)的交錯和是\(9-6+4-2+1=5\)。\(\{\;5 \}\;\)的交錯和是5)。求全部"交錯和"的總和\(S\)。
解 直接從定義入手去計算\(S\),顯然是困難重重。我們尋找另一種計算\(S\)的方法。
從元素入手。每一個小於\(n\)的元素\(a\),如果在不含\(n\)的子集\(A\)中,那麼它也在含\(n\)的子集\(\{\;n \}∪A\;\)中,反之亦然。如果它對集合\(A\)的交錯和貢獻為\(+a\)(若\(-a\)),那麼它對集合\(\{\;n \}∪A\;\)的交錯和貢獻為\(+a\)(若\(-a\)),反之亦然。於是,\(a\)對各個子集的交錯和貢獻兩兩抵消。\(a\)對於總和\(S\)的貢獻為0。
元素\(n\),對每個含\(n\)的子集的交錯和,貢獻為\(n\)。而含\(n\)的子集有\(2^{n-1}\)個。所以\(n\)對總和\(S\)的貢獻為\(n\cdot 2^{n-1}\)。綜上所述,\(S=n\cdot 2^{n-1}\)。
(單墫,算兩次P54)
\(M\)是集合\(S=\{\;1,2,3,\ldots,9 \}\;\)的子集,將\(M\)中各元素由大到小排列,最大的數維持原值,次大的數變號,第三大的數又維持原值,第四大的數變號,\(\ldots\),再將經過這種程序處理過的數相加,稱為\(M\)的交錯和。(例如\(M=\{\;9,7,4,3,1 \}\;\),則其交錯和為\(9-7+4-3+1=4\))。求所有\(S\)的子集的交錯和的和。
(96南港高工日間部)
對於{1,2,3,4,5,6,7}的每一個非空子集,我們將子集內的元素依遞減排列,且正負號依序交錯,並計算其值。舉例來說,對於子集{5} 我們得到 5;對於子集{6 , 3 , 1} 我們得到6-3+1=4;試求所有的結果數字的總和是多少?
https://math.pro/db/thread-3073-1-1.html
\(X\)為有限集合,定義函數\(f(X)\)為\(X\)內最大的數,減第二大的數,加第三大的數,減第四大的數,\(\ldots\),依此類推。
例如:\(f(\{\;3,6,10,1 \}\;)=10-6+3-1=6\),\(f(\{\;3,6,10,2,4 \}\;)=10-6+4-3+2=7\)。若\(A=\{\;1,2,3,4,\ldots,112 \}\;\),而\(X\)為\(A\)中的非空子集,則所有\(f(x)\)的和為
。
(112台北市高中聯招,
https://math.pro/db/thread-3729-1-1.html)