在1781 年,日本藤田貞資於《精要算法》中提出所謂「蟲蝕算」這種填字遊戲。顧名思義,蟲蝕算遊戲就是將算式中打□被蟲損傷的地方,根據算術或代數推理手段恢復原來的數字使等式成立。下圖是一道稱為〈一個8〉的蟲蝕算遊戲:
☐☐☐
✕ 8☐
----
☐☐☐☐
☐☐☐
----
☐☐☐☐
試問:這道遊戲的最後四個數字為
。
(109高中數學能力競賽 北一區複試筆試二)
(108新北市高中聯招,
https://math.pro/db/viewthread.php?tid=3133&page=6#pid19979)
―――――――――――――――――――――――――――
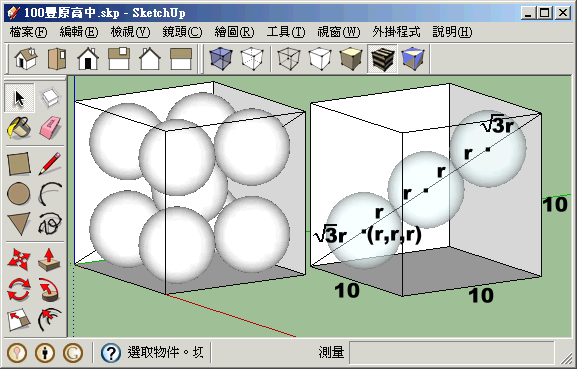
邊長 4 的正方體內擺放八個半徑相同的球體,在此八個球體半徑最大的情形下,在他們中間放置一個小球,求此小球的最大半徑。
(109高中數學能力競賽 北一區口試)
更多類似問題
https://math.pro/db/thread-1268-1-1.html
―――――――――――――――――――――――――――
超過2020的正整數中,恰有14個正因數的最小數是
。
(109高中數學能力競賽 北二區複試筆試二)
求有30個正因數的最小正整數。
(106學年度第1學期中山大學雙週一題)
―――――――――――――――――――――――――――
現有\(A\)、\(B\)兩個水桶,我們利用以下規則交換兩個水桶的水:我們從\(A\)水桶取出2/3的水,從B水桶取出全部的水,並且將這些取出來的水倒入另一個水桶。現在假設\(A\)水桶裝水1公升,B水桶裝水2公升,不斷重複上述規則,請問\(A,B\)兩水桶的水量分別會趨近為
。
(109高中數學能力競賽 北二區複試筆試二)
―――――――――――――――――――――――――――
設\(x,y\)為實數。已知\(y^2\ge 1\)且滿足\((\sqrt{1+x^2}-x)(y-\sqrt{y^2-1})=1\),試求\(x^2-y^2=\)
。
(109高中數學能力競賽 北二區複試筆試二)
\( (a+\sqrt{a^2+4})(b+\sqrt{b^2+9})=16 \),求\( a \sqrt{b^2+9}+b \sqrt{a^2+4} \)。
(100南科實中,
https://math.pro/db/thread-1153-1-1.html)
―――――――――――――――――――――――――――
滿足\((x^2-21x+109)^{x^2-212x+2020}=1\)的所有實數\(x\)之總和為
。
(109高中數學能力競賽 臺北市複試筆試二)
方程式\( (x^2-3x+1)^{x+1}=1 \)有幾個整數解?
(98彰化女中,
https://math.pro/db/viewthread.php?tid=741&page=1#pid1294)
―――――――――――――――――――――――――――
若實數\(\alpha\)與\(\beta\)滿足\(\cases{\alpha^3-6\alpha^2+13\alpha=2020 \cr \beta^3-3\beta^2+4\beta=-2008}\),則\(\alpha+\beta=\)
。
(109高中數學能力競賽 台北市複試筆試二)
\( \Bigg\{\; \matrix{(x-1)^3+(x-1)(2016)=-105 \cr (y-1)^3+(y-1)(2016)=105} \),求\( x+y= \)
。
(105師大附中代理,
https://math.pro/db/thread-2543-1-1.html)
―――――――――――――――――――――――――――
函數\(f\)的定義為\(f(x,y)=x^2+4xy-10x+5y^2-24y+35\),其中\(x,y\)為實數。則函數\(f\)的最小值為
。
(109高中數學能力競賽 新北市複試筆試二)
類似問題
https://math.pro/db/viewthread.php?tid=680&page=3#pid7957
―――――――――――――――――――――――――――
西元2019年9月,布克與薩瑟蘭兩位數學家發現42可以寫成下面三整數的立方和:
\((−80538738812075974)^3+(80435758145817515)^3+n^3 = 42\).其中正整數\(n\)的最末兩位數為
。
(109高中數學能力競賽 新北市複試筆試二)
三立方和整數解
http://mathland.idv.tw/history/sums_of_three_cubes.htm
―――――――――――――――――――――――――――
平面有一個凸10邊形,連接其所有對角線,最多可以把此10邊形的內部分為
塊區域。
(109高中數學能力競賽 新北市複試筆試二)
[公式]
\(C_0^n+C_2^n+C_4^n-n\)
凸10邊形,把每條對角線都連上,最多可以把此10邊形內部分為幾塊區域?
(A)256 (B)246 (C)200 (D)128
(109新北市國中聯招,
https://math.pro/db/thread-3346-1-1.html)
―――――――――――――――――――――――――――
設\(n\in N\),\(n\ge 2\),令\(\displaystyle A_n=\sum_{k=1}^n \frac{k}{1+k^2+k^4}\),\(\displaystyle B_n=\prod_{k=2}^n \frac{k^3-1}{k^3+1}\),求\(A_n\cdot B_n\)。
(109高中數學能力競賽 中投區複試筆試一)
\(\displaystyle A_n=\sum_{k=1}^n \frac{k}{1+k^2+k^4}=\sum_{k=1}^n \frac{k}{(k^2-k+1)(k^2+k+1)}=\sum_{k=1}^n \frac{1}{2}\left(\frac{1}{k^2-k+1}-\frac{1}{k^2+k+1}\right)\)
(我的教甄準備之路 裂項相消,
https://math.pro/db/viewthread.php?tid=661&page=2#pid1678)
―――――――――――――――――――――――――――
設\(\Delta ABC\)滿足\(cosA:cosB:cosC=1:1:2\),求\(sinA\)。
(109高中數學能力競賽 中投區複試筆試二)
感謝satsuki931000告知出處
設三角形\(ABC\)滿足\(cosA:cosB:cosC=1:1:2\)。將\(sinA\)表示為\(\root s \of t\),其中\(s\)為正整數,\(t\)為正有理數且為最簡分數。試問:\(s+t=\)
(化為最簡分數)。
(2020APMO初選試題,
http://imotwn.math.ncu.edu.tw/topics/APMO)
\(\Delta ABC\),\(cosA:cosB:cosC=25:39:(-3)\),求\(a:b:c\)。
(102內湖高中,
https://math.pro/db/viewthread.php?tid=1621&page=1#pid8281)
―――――――――――――――――――――――――――
一個凸四邊形\(ABCD\)如圖所示,其中\(∠ABC=135^{\circ}\),\(∠BCD=120^{\circ}\),\(\overline{AB}=\sqrt{6}\),\(\overline{BC}=6-\sqrt{3}\),\(\overline{CD}=6\),求\(\overline{AD}\)之長度。
(109高中數學能力競賽 中投區複試筆試二)
(114建功高中,
https://math.pro/db/thread-3942-1-1.html)
四邊形\(ABCD\)中,\(\overline{AB}=5\),\(\overline{AD}=3\sqrt{2}\),\(\overline{CD}=4\sqrt{3}\),\(∠BAD=135^{\circ}\),\(∠ADC=105^{\circ}\),則其面積為何?
(建中通訊解題第90期)
―――――――――――――――――――――――――――
正方形\(ABCD\)的邊長為2,點\(E\)和\(F\)分別在邊\(BC\)和\(CD\)上,使得\(\Delta CEF\)的周長為4,試求:
(1)\(∠EAF\)的度數;
(2)\(\Delta EAF\)面積的最小值。
(109高中數學能力競賽 台南市複試筆試一)
―――――――――――――――――――――――――――
求方程式\(\displaystyle \frac{x+y}{x^2-xy+y^2}=\frac{3}{13}\)的所有整數解。
(109高中數學能力競賽 台南市複試筆試二)
設\(x,y\)為整數,\(x\ge y\)且滿足方程式\(\displaystyle \frac{x+y}{x^2-xy+y^2}=\frac{3}{7}\),求數對\((x,y)\)?
(94年高中數學能力競賽決賽獨立研究(一)試題,95基隆高中,建中通訊解題第64期)
―――――――――――――――――――――――――――
試求\(\displaystyle \frac{1}{2} \{\;(sin15^{\circ}+\sqrt{(sin15^{\circ})^2-1})^{2020}+(sin15^{\circ}-\sqrt{(sin15^{\circ})^2-1})^{2020} \}\;\)之值。
(109高中數學能力競賽 高雄市複試筆試一)
―――――――――――――――――――――――――――
已知實數\(a,b,c\)滿足下列條件:
\(\cases{\displaystyle \frac{a}{1^2+2^2}+\frac{b}{2^2+3^2}+\frac{c}{2^2+5^2}=1\cr
\frac{a}{1^2+4^2}+\frac{b}{3^2+4^2}+\frac{c}{4^2+5^2}=1\cr
\frac{a}{1^2+6^2}+\frac{b}{3^2+6^2}+\frac{c}{5^2+6^2}=1}\)
試求\(a+b+c\)之值。
(109高中數學能力競賽 高雄市複試筆試一)
若對\( n=4,6,8,10 \),實數\(a,b,c,d\)滿足\( \displaystyle \frac{a^2}{n^2-3^2}+\frac{b^2}{n^2-5^2}+\frac{c^2}{n^2-7^2}+\frac{d^2}{n^2-9^2}=1 \),求\(a^2+b^2+c^2+d^2=\)?
(105彰化高中,
https://math.pro/db/viewthread.php?tid=2492&page=1#pid15192)
―――――――――――――――――――――――――――
已知\(x,y,z\)是正數且滿足\(\cases{2x+2y+xy=18 \cr 2y+2z+yz=20 \cr 2x+2z+xy=29}\),試求\(x+y+z+xyz\)之值。
(109高中數學能力競賽 高雄市複試筆試二)
―――――――――――――――――――――――――――
求證:\(\displaystyle \left(1+\frac{1}{n}\right)^n<\left(1+\frac{1}{n+1}\right)^{n+1}\),\(n\)為正整數。
(109高中數學能力競賽 高屏區複試口試)