我忘記題目有沒有提到頂點順序了
應該每個情況都試才對
經過確認，最大值=√5+2(發生在S=P+Q-R
感謝   d3054487667之確認
前面提供的方法已更新

另外R對應的複數 有共軛

[ 本帖最後由 Almighty 於 2019-4-17 00:27 編輯 ]

謝謝thepaino老師回答

引用:

原帖由 Almighty 於 2019-4-16 23:54 發表
我忘記題目有沒有提到頂點順序了
應該每個情況都試才對
經過確認，最大值=√5+2(發生在S=P+Q-R
感謝   d3054487667之確認
前面提供的方法已更新

另外R對應的複數 有共軛 ...

題目有說以PQ, PR為兩邊,所以 PSQR這個組合不行吧

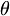
另外 P+R-Q= (2a+b)+i(-a-2b) ,所以 \(\overline{OS}^2\)=5+4sin2\(\theta\)  所以OS最大值也是3 吧

R是對應 \(2\overline{z}\)

另外想請問第9題

我的想法是先算出平面PQR的法向量是(1,1,-1) 所以考慮 P+t(1,1,-1) , Q+t(1,1,-1) , R+t(1,1,-1) 皆會落在表面上, 算出來t=1/2

所以三角柱的高就是1/2* |(1,1,-1)|=根號3/2

不曉得這想法對不對

感謝老師的分享！小弟瞭解了

填充9.
在邊長為1的正立方體\(ABCD-A_1B_1C_1D_1\)中，\(P,Q,R\)分別為\(\overline{AB},\overline{AD},\overline{AA_1}\)的中點，以\(\Delta PQR\)為底面做一個直三角柱，使其另一個底面的三個頂點也都在正立方體\(ABCD-A_1B_1C_1D_1\)的表面上，則這個直三角柱的體積為　　　。

並且回應g112老師，以下是我的作法

想對一下計算四第一題的答案
小弟的答案是 \(25x^{2}-28xy+8y^{2}=4\)

逆時針旋轉 45 度後，不會有 xy 項吧？

計算4.
在坐標平面上，將\(\Gamma\)：\(5x^2+14xy+13y^2=8\)之圖形沿著\(x\)軸推移\(y\)坐標之2倍後，再以原點為中心逆時針旋轉\(45^{\circ}\)得新圖形\(\Gamma'\)，求
(1)\(\Gamma'\)之方程式。
(2)若\(P(x,y)\in \Gamma\)，求\(P\)到\(L\)：\(3x+y=10\)的最短距離。

計算題四，下列解法2應該是最簡單又最快的，但因為有第(1)小題制約反而不容易想到QQ
另外，我記得題目給的直線是  3x+y=10 ，而不是x+3y=10；
算法雖然一樣，但數字稍微好看一點點。

知道哪邊算錯了 感謝兩位老師

是說swallow7103老師第2個方法應該可以直接使用 給定切線斜率求橢圓切線的公式

橢圓\(a=1\) \(b=2\)  注意直線要經過伸縮轉換得到\(y=4x-5\sqrt{2}\)
令切線\(L:y=4x\pm \sqrt{a^2m^2+b^2}\)
代入數字得\(L:4x\pm 2\sqrt{5}\)
取\(L:y=4x-2\sqrt{5}\)
最短距離為L和\(y=4x-5\sqrt{2}\)的距離

故答案為\(\sqrt{10}-2\)

再次感謝兩位老師的指教

[ 本帖最後由 satsuki931000 於 2019-4-21 10:56 編輯 ]

\(y=4x-2\sqrt{5}\) 與 \(y=4x-5\sqrt{2}\) 的距離不是 \(\sqrt{10}-2\)