1.兩正數\( \displaystyle a=\frac{1}{1 \times 2}+\frac{1}{3 \times 4}+\frac{1}{5 \times 6}+...+\frac{1}{2003 \times 2004} \)
\( \displaystyle b=\frac{1}{1003 \times 2004}+\frac{1}{1004 \times 2003}+\frac{1}{1005 \times 2002}+...+\frac{1}{2004 \times 1003} \)
則\( \displaystyle \frac{a}{b}= \)?(請化為最簡分數)
[出處,93高中數學能力競賽 第二區筆試二試題]
\( \displaystyle a=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2003}-\frac{1}{2004} \)
\( \displaystyle a=\frac{1}{1}+\frac{1}{2}+...+\frac{1}{2004}-2(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2004}) \)
\( \displaystyle a=\frac{1}{1003}+\frac{1}{1004}+...+\frac{1}{2004} \)
頭尾相加
\( \displaystyle a=\frac{3007}{1003 \times 2004}+\frac{3007}{1004 \times 2003}+...+\frac{3007}{1503 \times 1504} \)
\( \displaystyle a=3007 \Bigg(\; \frac{1}{1003 \times 2004}+\frac{1}{1004 \times 2003}+...+\frac{1}{1503 \times 1504} \Bigg)\; \)
\( \displaystyle b= \Bigg(\; \frac{1}{1003 \times 2004}+\frac{1}{1004 \times 2003}+...+\frac{1}{1503 \times 1504}\Bigg)\;+\Bigg(\; \frac{1}{1504 \times 1503}+\frac{1}{1505 \times 1502}+...+\frac{1}{2004 \times 1003} \Bigg)\; \)
\( \displaystyle b=2 \Bigg(\; \frac{1}{1003 \times 2004}+\frac{1}{1004 \times 2003}+...+\frac{1}{1503 \times 1504} \Bigg)\; \)
111.4.25補充
已知\(\displaystyle p=\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+\ldots+\frac{1}{2021\times 2022}\),
\(\displaystyle q=\frac{1}{1012\times 2022}+\frac{1}{1013\times 2021}+\frac{1}{1014\times 2020}+\ldots+\frac{1}{2022\times 1012}\),試求\(\displaystyle \frac{p}{q}\)之值=
。
(111臺南一中,
https://math.pro/db/thread-3635-1-1.html)
5.橢圓\( \displaystyle \frac{(x-21)^2}{21}+\frac{(y-100)^2}{100}=2100 \)在第一、二、三、四象限內的面積依次為\( R_1 \)、\( R_2 \)、\( R_3 \)、\( R_4 \),則\( R_1-R_2+R_3-R_4= \)?
[提示]
高中數學101 P238,高中數學101修訂版 P240有這題
中心在\( (x_0,y_0) \),\( R_1-R_2+R_3-R_4=4 |\ x_0 y_0 |\ \)
7.如下圖,正三角形△ABC,若D,E,F將三邊分成\( \overline{AF}:\overline{FB}=\overline{BD}:\overline{DC}=\overline{CE}:\overline{EA}=2 : (n-2) \);
(其中\( n>4 \)),且\( \overline{AD} \),\( \overline{BE} \),\( \overline{CF} \)相交所成的△PQR的面積是△ABC的\( \displaystyle \frac{1}{7} \),則n值為?
如右圖,△ABC中,D,E,F分別為三邊之三等分點,\( \overline{AD} \),\( \overline{BE} \),\( \overline{CF} \)兩兩分別交於P,Q,R,△PQR和△ABC面積比為何?
(97大安高工)
這題答案就是1:7,2: (n-2)=1:2,n=6
假如沒背到這題答案的話,原本的方法是
\( \overline{AF}:\overline{FB}=\overline{BD}:\overline{DC}=\overline{CE}:\overline{EA}=1:t \)
\( \displaystyle △ABQ=\frac{1+t}{1+t+t^2}△ABD \),\( \displaystyle △ABD=\frac{t}{1+t}△ABC \)得\( \displaystyle △ABQ=\frac{t}{1+t+t^2}△ABC \)
最後可得到\( \displaystyle △PQR=\frac{1-2t+t^2}{1+t+t^2}△ABC \),得\( t=2 \)
以上的解法出自 國際數學奧林匹克大陸隊訓練教材 P136
101.2.11補充資料
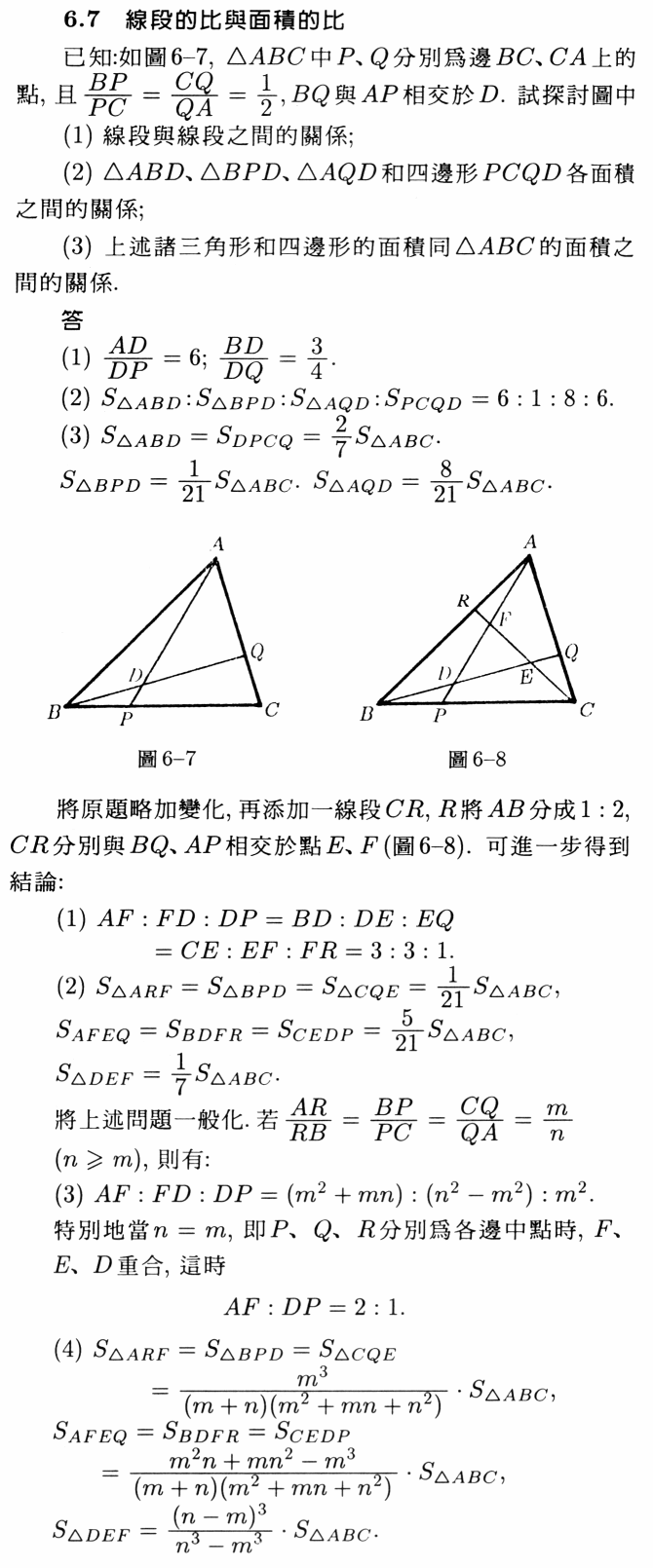
已知:如圖6-7,△ABC中P、Q分別為邊\( \overline{BC} \)、\( \overline{CA} \)上的點,且\( \displaystyle \frac{\overline{BP}}{\overline{PC}}=\frac{\overline{CQ}}{\overline{QA}}=\frac{1}{2} \),\( \overline{BQ} \)與\( \overline{AP} \)相交於D。試探討圖中
(1)線段與線段之間的關係;
(2)△ABD、△BPD、△AQD和四邊形PCQD各面積之間的關係;
(3)上述諸三角形和四邊形的面積同△ABC的面積之間的關係。

101.12.18
補充另外一種解法
宋釗宜,難解數學破題
 面積比.rar (7.83 KB)
面積比.rar (7.83 KB)
102.9.20補充
若\( \displaystyle \frac{AR}{RB}=\frac{BP}{PC}=\frac{CQ}{QA}=\frac{m}{n} \)則有
(3)\( AF:FD: DP=(m^2+mn): (n^2-m^2):m^2 \)
感謝thepiano解題
http://www.shiner.idv.tw/teachers/viewtopic.php?f=46&p=9976
102.11.20補充
https://math.pro/db/viewthread.php?tid=206&page=2#pid9415

105.5.20補充
任意給定一個三角形\(ABC\),已知\(P、Q、R\)分別為\(\overline{AB}\)、\(\overline{BC}\)、\(\overline{CA}\)三邊上的三點,且\(\overline{AP}:\overline{PB}=\overline{BQ}:\overline{QC}=\overline{CR}:\overline{RA}=2:1\),若\(\overline{CP},\overline{AQ},\overline{BR}\)兩兩交於點\(A',B',C'\)。求\(\Delta A'B'C'\)與\(\Delta ABC\)的面積比。
(建中通訊解題 第92期)
111.1.11補充
在三角形\(ABC\)的三邊\(\overline{BC}\)、\(\overline{CA}\)、\(\overline{AB}\)上依次取\(D\)、\(E\)、\(F\)點,且使\(\overline{BD}:\overline{DC}=\overline{CE}:\overline{EA}=\overline{AF}:\overline{FB}=1:2\),令\(\overline{AD}\)與\(\overline{CF}\)交於\(P\)點,\(\overline{BE}\)與\(\overline{AD}\)交於\(Q\)點,\(\overline{CF}\)與\(\overline{BE}\)交於\(R\)點,求\(\Delta ABC\)與\(\Delta PQR\)的面積比。
(106羅東高中,
https://math.pro/db/thread-2801-1-1.html)
在(圖一)中,\(\displaystyle \overline{TQ}=\frac{1}{2}\overline{ST}\),\(\displaystyle \overline{UR}=\frac{1}{3}\overline{TU}\),\(\displaystyle \overline{SP}=\frac{1}{4}\overline{SU}\)。已知\(\Delta STU\)的面積是1。則\(\Delta PQR\)的面積為
。
(98嘉義高中,
https://math.pro/db/thread-2417-1-1.html)
8.x為實數時,若\( \displaystyle f(x)=\frac{ax^2+x+1}{x^2+x+a} \)為所有實數,則常數a之範圍為?
(93高中數學能力競賽 雲嘉區筆試二試題)
h ttp://www.math.nuk.edu.tw/senpe ... _High_ChiaYi_02.pdf 連結已失效
9.擲一公正骰子200次,若至少出現100次正面的機率為\( \displaystyle a+(\frac{1}{2})^k C_{100}^{200} \),則數對\( (a,k)= \)?
h ttp://forum.nta.org.tw/oldphpbb2/viewtopic.php?t=41934 連結已失效
17.n是自然數,O為原點,平面π: \( x+ny+(n+2)z=1 \)與三坐標軸相交於點\( A_n \),\( B_n \),\( C_n \),若\( V_n \)表四面體\( O-A_nB_nC_n \)的體積,求\( \displaystyle \sum_{n=1}^{\infty}V_n= \)?
[提示]
高中數學101 P186,高中數學101修訂版 P187有這題
\( \displaystyle \frac{x}{1}+\frac{y}{\frac{1}{n}}+\frac{z}{\frac{1}{n+2}}=1 \)
\( \displaystyle A_n=(1,0,0) \),\( \displaystyle B_n=(0,\frac{1}{n},0) \),\( \displaystyle C_n=(0,0,\frac{1}{n+2}) \)
19.\( \displaystyle \int_0^2 \lim_{n \to \infty} \frac{(2-x)(x+x^n)}{1+x^n}dx \)之值為?
(99中正預校,
https://math.pro/db/thread-990-1-1.html)
解答在
http://www.shiner.idv.tw/teacher ... &start=10#p4039