感謝thepiano和Ellipse提供題目出處
1.
某一燈塔裝置了紅、黃、藍、綠、紫五種不同顏色的燈,每晚會點亮其中一種燈,且每一晚都是從前一晚未點過的四種燈中隨機點亮一種。設第1晚點亮紅色燈,則第6晚也點亮紅色燈的機率為
(以最簡分數表示)。
(102高中數學能力競賽 北一區(花蓮高中)筆試二試題,
https://math.pro/db/thread-2359-1-1.html)
2.
設集合\(A=\{\;1,2,3,\ldots,102 \}\;\)共102個數,\(B\)、\(C\)為另2個集合,滿足\(B∪C=A\),則這樣的\((B,C)\)共有
。
(102高中數學能力競賽 北一區(花蓮高中)筆試二試題,
https://math.pro/db/thread-2359-1-1.html)
3.
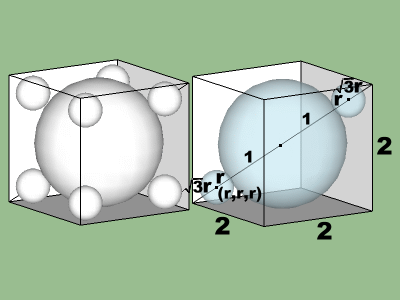
一模型公司在一個內部邊長為2單位的透明正立方體箱子內,放置一顆半徑為1單位的黃球,然後又要在箱子的八個角落再塞入8顆半徑相同的小紅球。試求:小紅球的最大半徑為
單位。
(102高中數學能力競賽 北一區(花蓮高中)筆試二試題,
https://math.pro/db/thread-2359-1-1.html)
100華江高中二招,
https://math.pro/db/viewthread.php?tid=1177&page=1#pid3990
102高中數學能力競賽,
https://math.pro/db/thread-2359-1-1.html
4.
設\(a\)、\(b\)為正整數,若\(a^{20}\)為31位數,\(\displaystyle \left(\frac{1}{b}\right)^{20}\)自小數點以下25位才不為0,則\((ab)^5\)是
位數。
(104高中數學能力競賽 北一區(花蓮高中)筆試二試題,
https://math.pro/db/thread-2466-1-1.html)
5.
將10個相同的小球裝入3個編號為1、2、3的盒子(每次要把10個球裝完),要求每個盒子裡球的個數不少於盒子的編號數,這樣的裝法種數共有
種。
(104高中數學能力競賽 北一區(花蓮高中)筆試二試題,
https://math.pro/db/thread-2466-1-1.html)
6.
設\(Q_1\)、\(Q_2\)為以原點\(O(0,0)\)為圓心的單位圓和\(x\)軸的兩交點。若上半圓上兩點\(P_1\)和\(P_2\)滿足\(∠P_1OP_2=45^{\circ}\),則\(\Delta P_1OQ_1\)和\(\Delta P_2OQ_2\)面積和的最大值為
。
(105台灣師大申請入學筆試二試題,
http://www.math.ntnu.edu.tw/down ... 6%E8%A9%A6%E4%BA%8C)
9.
級數\(\displaystyle \sum_{k=0}^{\infty}\frac{(-2)^k}{(2^{k+1}+(-1)^{k+1})(2^k+(-1)^k)}\)之和為有理數,此有理數最簡分數為
。
[提示]
待定係數法
設\(\displaystyle \frac{(-2)^k}{(2^{k+1}+(-1)^{k+1})(2^k+(-1)^k)}=\frac{a\cdot 2^{k+1}}{2^{k+1}+(-1)^{k+1}}-\frac{a\cdot 2^k}{2^k+(-1)^k}\),得\(\displaystyle a=\frac{1}{3}\)
\(\displaystyle \frac{(-2)^k}{(2^{k+1}+(-1)^{k+1})(2^k+(-1)^k)}=\frac{1}{3}\left(\frac{2^{k+1}}{2^{k+1}+(-1)^{k+1}}-\frac{2^k}{2^k+(-1)^k}\right)\)
(我的教甄準備之路 裂項相消,
https://math.pro/db/viewthread.php?tid=661&page=2#pid1678)
計算證明題1.
將長\(\overline{AB}=240\),寬\(\overline{BC}=288\)的長方形紙張對摺,讓頂點\(C\)剛好落在線段\(\overline{AB}\)的中點\(M\)上,若\(\overline{EF}\)是摺線,則摺線\(\overline{EF}\)的長度為多少?
(101高中數學能力競賽 花蓮區筆試一試題,
http://pisa.math.ntnu.edu.tw/fil ... s_writtenexam_1.pdf)
類似題
\(ABCD\)是邊長為1的正方形,沿\(\overline{PQ}\)對折,使得\(A,B\)對折之後分別重合於\(A',B'\)兩點,且\(B'\)在\(\overline{CD}\)上,
(a)證明\(\Delta RB'D\)的周長為2。
(b)求\(\Delta QB'C\)的最大面積。
(97國立大里高中,
https://math.pro/db/thread-2402-1-1.html)
109.10.2補充
摺到中點時,各線段的比例
https://books.google.com.tw/book ... ge&q&f=true
Origamics: Mathematical Explorations Through Paper Folding

