D.
設
a b
b c
c為正實數,試求
2b−2ca+b+2c+2a+4ca+2b+c+ba+b+c的最小值
。
連結有解答
(建中通訊解題 第61期,連結已失效h ttp://web2.ck.tp.edu.tw/~mathweb/index.php?option=com_content&view=article&id=42:2012-02-07-02-50-11&catid=19:2011-11-23-08-30-15&Itemid=37)
F.
設有一階梯共有20階,每次只能走2階或3階,第8階階梯壞掉不能踩且必須踩上第12階的上樓方法數為
。
(101中科實中,
https://math.pro/db/viewthread.php?tid=1318&page=2#pid5048)
G.
球體
S:x2+y2+z2 4
4被平面
E:3x+2y+2 3z=5
3z=5 割成兩部份,求較小部份的體積為
。
https://math.pro/db/viewthread.php?tid=951&page=2#pid2258
I.
已知三次方程式
x3−2x2−6x+5=0的三根分別為


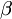

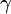
,則
 5+
5+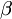 5+
5+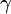 5=
5= 。
[公式]
f(x)f (x)
(x)
數學傳播第七卷第四期,林文東,一元n次方程式根的同次冪之和的求法
https://math.pro/db/viewthread.php?tid=680&page=2#pid2434可下載文章
K.
凸12邊形的任意3條對角線不交於12邊形內一點,求這些對角線將凸12邊形分成
個區域數。
[公式]
C0n+C2n+C4n−n
已知一個凸八邊形中的任意3條對角線不交於形內一點,求這些對角線將凸八邊形分成的區域的個數?
(建中通訊解題第55期)
上面題目問區域數,下面題目問三角形個數?
平面上凸n邊形之對角線沒有三線共點者,則由此凸n邊形之邊與對角線所圍出三角形個數
[公式]
C3n+4C4n+5C5n+C6n
https://math.pro/db/thread-624-1-1.html
O.
有一個遊戲叫做「九宮格」,就是被叫到的人,其座位周圍在九宮格內的人都要站起來,如右圖,座位標示「●」被叫到時,周邊標示「☆」的人都要站起來。
由例二得知,坐在最外層的人被叫到時,要站起來的人數會比較少。今已知甲乙兩位學生在同一班,而該班學生共有5×5位,則當兩人任意坐時,當甲被叫到而乙必須站起來的機率為
。
96高中模擬考,連結已失效h ttp://www.tcgs.tc.edu.tw/~sunp/simulate/math/Taipei/964mathA.pdf
P.
三角形的三邊長分別為
 29
29 、
 37
37 、
 52
52 ,求此三角形面積為
。
(建中通訊解題 第38期)
T.
已知實數
a b
b c
c滿足
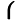
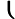
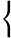

 a(4−b)=4b(4−c)=4c(4−a)=4
a(4−b)=4b(4−c)=4c(4−a)=4,則
a+b+c= 。
輪換方程式,將題目整理到這裡
https://math.pro/db/thread-2020-1-1.html
U.
長方形如右圖,
E、
F分別在
AB、
BC邊上,已知
 ADE
ADE、
 BEF
BEF、
 CDF
CDF的面積分別為2、3、4,則
 DEF
DEF的面積為
。
連結已失效h ttp://www.mathland.idv.tw/life/rectri.pdf