附件是記憶中的題目
有些敘述不太完整，有的數字可能不對，

或是寸絲的中文不好，言不及意

還請各位幫忙指正，謝謝~~

感謝 lianger 幫忙修正題意和題號

請諸位慢慢享用

感謝分享

3.
曲線Γ：y=x1，
(1)△ABC三頂點皆在曲線Γ 上，求證其垂心亦在曲線Γ上。
(2)D=(−1−1)，△BCD為正三角形，且B,C在第一象限曲線Γ上。求B,C坐標。
https://math.pro/db/thread-559-1-1.html
在最後一題加分題有解答
連結已失效h ttp://web.tcfsh.tc.edu.tw/math/math2/T95221A.pdf

設雙曲線xy=1的兩支為C1C2，正三角形PQR的三頂點位於此雙曲線上。
(1)求證：P,Q,R不能都在雙曲線的同一支上。
(2)設P(−1−1)在C2上，Q,R在C1上，求頂點Q,R的坐標。
(1997大陸高中數學聯合競賽)

4.
我覺得題目要改成這樣才算得出來
(1)f(x)=−x2+68x−256−−x2+10x−9 ，求f(x)的最大值。
(2)承上，此時x之值。
[解答]
(x-34)^2+y^2=30^2的上半圓為y=−x2+68x−256 
(x-5)^2+y^2=4^2的上半圓為y=−x2+10x−9 
此時f(x)可視為兩半圓的y值相減的函數，當x=9時有最大值511 

感謝lianger和tsusy指教，原來用加的也是可以解出來

Find the largest positive value attained by the function f(x)=8x−x2−14x−x2−48 , x a real number
(A)7−1 　(B)3　(C)23 　(D)4　(E)55−5 
(1993AHSME，http://www.artofproblemsolving.c ... 82&cid=44&year=1993)

設xR，試求f(x)=8x−x2−14x−x2−48 的最大值？
(96和美高中，96基隆海事)

5.
xn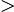正實數數列，x1=43且滿足x2k+1=x4k+2x3k+x2k，求1x1+1+1x2+1++1x202+1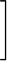 

有一個數列x1,x2,x3,…,x2001，其中x1=31且xk+1=x2k+xk，k=122000請找出1x1+1+1x2+1+1x3+1++1x2001+1的整數部分？
(建中通訊解題第11期)

10.
求所有的正實數x,y，滿足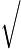2x2+y2 ，2x+y，xy ，2xyx+y皆為正整數且四數之和為66。

感謝thepiano將這麼古老的討論文章挖了出來
http://www.shiner.idv.tw/teachers/viewtopic.php?t=2814
h ttp://forum.nta.org.tw/examservice/showthread.php?t=8852 (連結已失效)

第4題
這題我在考試的時候也沒湊出來，後來才想到可以用柯西不等式，沒拿到這10分真是太可惜了!
f(x)=(x−1)(9−x)+(64−x)(x−4)=x−19−x+64−xx−4 
(x−1)(9−x)  0(64−x)(x−4)0 
  4  x9
所以x−1，9−x，64−x，x−4皆不小於0
由柯西不等式得
[(x−1)+(64−x)][(9−x)+(x−4)](x−19−x+64−xx−4)2 
所以x−19−x+64−xx−4    635=335 
所求之最大值為335 
等號成立時，9−xx−1=x−464−x 
  x=17143

[ 本帖最後由 lianger 於 2012-5-20 12:10 PM 編輯 ]

lianger 是對的，小弟也算出同樣的 x

幾何解法，
取 (x−5)2+y2=42 的上半圓和 (x−34)2+(y−335)2=302  下半圓

兩半圓外切，而兩根號，可視為 半圓上的點至圓心的 y 分量，如圖 BD,  AC 之和

因此兩大值為兩圓心 y 坐標之差 335 , 其發生位置，其可由分點公式算出 x=17143

101panchiao.gif (496.76 KB)

2012-5-20 12:43

[ 本帖最後由 tsusy 於 2012-5-20 12:45 PM 編輯 ]

第八題的範圍印象中是　101 到 2012

因為當時我的解讀是  民國101年和西元2012年   XD

謝謝各位無私的分享
沒記錯的話
第8題n範圍為66<=n<=2012
第9題f(0)=1,f(1)-3,則積分0到1  (f''(x))^2dx>=4
不好意思,電腦能力太弱

感謝 sweeta 和 brace 兩位提供訊息

第 9 題 brace 的數字應該才是對的

而第 8 題，個人的印象是有 6 偶數...但 66 的話不就和最後一題一樣??這樣應該會有印象才是?

印象中第 8 題算出 90xxxx。 不知道，諸位對此數字是否有印象，也可能是小弟算錯

[ 本帖最後由 tsusy 於 2012-5-21 09:50 PM 編輯 ]

幫朋友解完第 5 題順便放上來~~

（聽他說，今年的彰中也有出一題類似題。）


第 5 題：

x2k+1=xkxk+12 

xk+1=xkxk+1 

1xk+1=1xkxk+1=1xk−1xk+1 

1xk+1=1xk−1xk+1


因為

1x1+1+1x2+1+    +1x202+1

=1x1−1x2+1x2−1x3+    +1x202−1x203 

=1x1−1x203 

1x1−0

=342


且


1x1+1+1x2+1+    +1x202+1

1x1+1+1x2+1+0+0+    +0

=143+1+14343+1+1 

=2592601

因此，

1x1+1+1x2+1+    +1x202+1=1 

應該是吧...昨天晚上也有人問寸絲

題目好像是 3an+1=a2n+3an，問的是 1an+3 的和之類的

手法一模一樣...昨天問小弟的那位，應該想撞牆了...

第九題:
考慮積分形式的柯西不等式:
若函數 f,g 在 [a,b] 可積分，則 (S (f(x))^2 dx) (S (g(x))^2 dx) 大於等於 (S f(x)g(x) dx)^2
(抱歉 其中的 S 表示積分符號， 且範圍為 [a,b]

本題中 (S (f'(x))^2 dx) (S 1^2 dx) 大於等於 (S f'(x) dx)^2, 其中 積分範圍為 [0,1]
化簡得到 (S (f'(x))^2 dx) 大於等於 (f(1)-f(0))^2 =4 , 驗畢.