引用:
原帖由 iamcfg 於 2011-6-26 05:04 PM 發表 
綜合7
先去算  與
與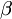 的長度關係 與 夾角
的長度關係 與 夾角
然後利用 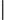
 −
−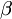
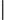 =2
=2 3可知道
3可知道 與
與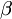 的距離
的距離
利用這兩點 可以得到 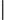

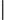 就可以算面積 ...
就可以算面積 ...
不好意思,提供個人淺見
這題解答內容上似乎有點問題
首先由b^2-2ab+4a^2=0,可得(b-a)^2=-3a^2
b-a=(+-)3^0.5*i*a
|b-a|=3^0.5*|a| -------------(1)
依題意知|b-a|=2*3^0.5
代入(1)得|a|=2--------------(2)
又
b=(1+3^0.5*i)a 或b=(1-3^0.5*i)a
|b|=2|a| =2*2=4
且
b=2[1/2 +(1/2)(3^0.5)i]a=2[cos(60度)+ i*sin(60度) ]a---------------------(3)
或b=2[1/2 -(1/2)(3^0.5)i]a=2[cos(-60度)+ i*sin(-60度) ]a------------------(4)
由 (3)知 將OA以O為圓心,逆時針旋轉60度可得到B點
由 (4)知 將OA以O為圓心,順時針旋轉60度可得到B點
它們都是角AOB=60度的三角形(並沒有夾角120度)
所求=(1/2)*2*4*sin60度 =2*3^0.5