第 13 題：將「南港愛我，我愛南港」8 個字全取排成一列，其中「南」與「港」兩字不相鄰之排法有＿＿＿種。

解答：

先排「我我愛愛」有 4!2!2!=6 種

然後再讓「南南港港」插空隙

可能的情況有四種「南南相鄰、港港相鄰」「南南相鄰、港港分開」「南南分開、港港相鄰」「南南分開、港港分開」

所以插空隙的方法有 C15C14+C15C24+C25C13+C25C23=110 種

所以，所求方法數為 6110=660 種。

請教第16題，有沒有類似的解法，謝謝。

問了蠢問題  自刪

[ 本帖最後由 JOE 於 2011-7-3 08:13 PM 編輯 ]

我用 矩陣算出 甲的期望值=16  所以乙的是=35-16=19

不知盲點在哪  請指教一下 謝謝!

第 16 題：（速解）

經長期互換多次後呈現穩定狀態後，

錢幣總額 10+10+5+5+5=35 元，均分給五個硬幣，

每個硬幣價值的期望值為 35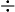5=7 元

乙袋有 3 個硬幣，所以期望值為 37=21 元。




另解：（比較慢一點，但是是標準作法）

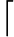
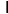
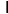
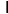
轉移矩陣 A=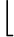31320312161010

其中上方的三的狀態分別是甲有 5+5元、10+5元、10+10元，

轉移後的左方三的狀態分別是甲有 5+5元、10+5元、10+10元。

長期而言，設達穩定狀態的矩陣為 P=xy1−x−y，

由 AP=P，可解得 x=310y=53，

所以，長期而言，甲袋中金額的期望值為 10310+1553+201−310−53=14 

乙袋金額的期望值為 35−14=21 元。



相同題目：99台中二中，https://math.pro/db/thread-934-1-1.html 計算第 5 題



103.03.22 補充 -----------------------------------------------------------------------------------------

有朋友跟我說他對轉移矩陣內的數字怎麼來的不太懂，補充說明如下：

甲有 5+5 （乙就有 10+10+5 元）

甲袋不管怎麼拿都會拿出 5 元

乙袋有 2/3 的機率拿到 10 元，有 1/3 的機率拿到 5 元，

因此，兩袋各取一枚硬幣交換的話，

有 1/3 的機率交換後，甲袋還是有 5+5 元。

有 2/3 的機率交換後，甲袋變成 10+5 元。

有 0 的機率（也就是不可能），甲袋會變成 10+10 元。

所以第一行的機率是 1/3, 2/3, 0


----------------------------------------

甲有 10+5 （乙就有 10+5+5 元）

甲袋有 1/2 的機率拿到 10 元，有 1/2 的機率拿到 5 元，

乙袋有 1/3 的機率拿到 10 元，有 2/3 的機率拿到 5 元，

因此，兩袋各取一枚硬幣交換的話，

有 (1/2)*(2/3)=1/3 的機率交換後（甲袋拿出10元，乙袋拿出5元來交換），甲袋會變成有 5+5 元。

有 (1/2)*(1/3)+(1/2)*(2/3)=1/2 的機率交換後（甲乙袋都拿出10元交換，或是甲乙袋都拿出5元來交換），甲袋還是有 10+5 元。

有 (1/2)*(1/3)=1/6 的機率（甲袋拿出5元，乙袋拿出10元來交換），甲袋會變成 10+10 元。

所以第一行的機率是 1/3, 1/2, 1/6

---------------------------------

同理，第三行留給你寫。

配方之後x=8分之3，而非4分之3吧?

由10−x20得到−10x  10 
再由10−x2(x+2)2得到-3<X<1
交集得-3<x<1

您將 10−x2x+2  兩邊同時平方的動作，做得太快了一點～

它與 10−x2(x+2)2 並不全然可以等價～

要是右邊負很多～左邊正很小～

像是當 −10x−3  時，這兩個不等式就沒有等價。




解答：

因為 10−x2  有意義，

所以 10−x20−10x10 

case i: 若 x+20 時，即 −10x−2  時，

　　　　因為 10−x20x+2  必成立，

　　　　得 −10x−2 。

case ii: 若 x+20，即 −2x10  時，

　　　　10−x2x+2010−x2(x+2)2 

　　　　−3x1，且因為 −2x10 

　　　　得 −2x1

由 case i&ii，可得 −10x1 

第 12 題：

|x|=\ 1
若f(x-3/x+1)+f(3+x/1-x)=x 求 f(x)

謝謝
試很久,都做不出來
請版上高手開釋一下

第 12 題：

已知 x=1，若 f(x+1x−3)+f(1−x3+x)=x，求 f(x)

解：

f(x+1x−3)+f(1−x3+x)=x ‧‧‧(i)

令 a=x+1x−3，則 x=1−a3+a

帶入（ｉ），可得 f(a)+f(a+1a−3)=1−a3+a

　　　　　　　即 f(x)+f(x+1x−3)=1−x3+x ‧‧‧(ii)

令 b=1−x3+x，則 x=b+1b−3

帶入（ｉ），可得 f(1−b3+b)+f(b)=b+1b−3

　　　　　　　即 f(1−x3+x)+f(x)=x+1x−3  ‧‧‧(iii)

由　［(iii)＋(ii)－(i)］／2，可得 f(x)=x3+7x2−2x2


ps. 1. 這是哪一間學校的題目呀？好像有看過這題！

　　2. 感謝 俞克斌 老師提醒我最後答案的計算錯誤。現已修正。：Ｄ