2.
解聯立方程祖
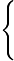 xy+x+y=−5x2+xy+y2=7
xy+x+y=−5x2+xy+y2=7 。
[提示]
令
x+y=a,
xy=b
同樣的技巧也能用在這題
解方程式
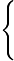 x+xy+y=2+3
x+xy+y=2+3 2x2+y2=6
2x2+y2=6 。
(99松山高中,
https://math.pro/db/thread-1044-1-1.html)
5.
已知
(1+x+x2)1000的展開式為
a0+a1x+

 +a2000x2000
+a2000x2000,試求
a0+a3+a6+

 +a1998=
+a1998=?
6.
用7個"+"號及5個"-"號排成一列,恰有4次變號的排法有多少種?
有3個「+」,4個「-」,排成一列。若一列中一個「+-」或一個「-+」我們說:有一個「變號」。問3個「+」,4個「-」排成一列,變號個數的期望值?
(98彰化女中,
https://math.pro/db/thread-741-1-1.html)
9.
若函數f滿足
f(93)=93,且對每一正整數n,
f(n)+f(n+3)=n2恆成立,則
f(30)=?
(2004TRML團體賽)
12.
x y
y為實數,已知
x2+xy+y2=3x+3y+9,若
x2+y2的最大值為M,最小值為N。求數對
(M N)=
N)=?
這裡可以找到答案
實數
x y
y滿足
x2+xy+y2=3(x+y+3),求
x2+y2之最大值與最小值?
(第七次合作杯數學有獎徵答,h ttp://web.tcfsh.tc.edu.tw/math/week.htm 連結已失效)
101.2.5補充
有一個大正立方體由27個單位立方體所組成,今有一個平面垂直且平分大正立方體內部之對角線,試問該平面與幾個單位立方體相交?
A large cube is formed by stacking 27 unit cubes. A plane is perpendicular to one of the internal diagonals of the large cube and bisects that diagonal. The number of unit cubes that the plane intersects is
(A)16 (B)17 (C)18 (D)19 (E)20
(1995AMC12,
http://www.artofproblemsolving.c ... id=44&year=1995)