6.
一模型公司在一個內部邊長為2單位的透明正立方體箱子內，放置一顆半徑為1單位的大球，然後又要在箱子的八個角落再塞入8顆半徑相同的小球。問：小球的最大半徑為
單位。
[提示]
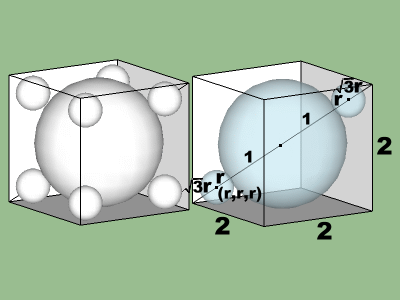SketchUp檔下載
一個邊長10cm的正立方體內塞九個大小相同的球，中心球的球心在正立方體的中心，其他球皆與三個相鄰面以及中心球相切，求球的半徑？
(100豐原高中，
https://math.pro/db/thread-1118-1-4.html)
9個相同的球被包裝在一個邊長為1的正立方體內，其中一個球的球心位於正立方體的中心點上，而其他的球均與中心球相切且與正立方體的三各面相切，則每一個球的半徑為 單位長。
(A)
1−2
3 (B)
223−3 (B)
62 (D)
41 (E)
423−6
(97全國高中聯招，h ttp://forum.nta.org.tw/examservice/showthread.php?t=48958網頁已失效)
感謝thepiano提示
http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&t=2612
109.6.22補充
109新北市高中聯招考了相同題目，
https://math.pro/db/thread-3351-1-1.html
7.
求值
49n=11
n+n2−1=？
(將答案化為最簡形式)
(我的教甄準備之路 裂項相消)
https://math.pro/db/viewthread.php?tid=661&page=2#pid1678
這題完全命中，連n=1到49都一模一樣，筆記裡有提示
8.
尤拉在1742年時，將白努力所舉的四次多項式
f(x)分解為二次多項式
x2−
2+4+27
x+1+4+27+7
與二次多項式
x2−2−4+27x+1−4+27+7
的乘積。白努利所舉的多項式
f(x)=
(以降次排列表示)
我嘗試著Maxima解題
https://math.pro/db/viewthread.php?tid=709&page=3#pid3989
110.2.21補充
方程式
X4−4X3+2X2+4X+4=0有四根
x1
2=1
2+i3 ，
x34=12−i3
(X−x1)(X−x3)=X2−(2+a)X+1+7+a
(X−x2)(X−x4)=X2−(2−a)X+1+7−a
a=4+27
https://books.google.com.tw/book ... ge&q&f=true
1743年尤拉回信給白努利
https://books.google.com.tw/book ... ge&q&f=true
計算證明題
1.
求
\displaystyle cot \frac{\pi}{24} 的值。
[提示]
\displaystyle cot \theta=\frac{cos \theta}{sin \theta}=\frac{2 cos^2 \theta}{2 sin \theta cos \theta}=\frac{1+cos 2 \theta}{sin 2 \theta}
2.
(2)試證：對每個大於1的整數n，恆有
\displaystyle \sqrt{2\sqrt{3\sqrt{4\sqrt{......\sqrt{n}}}}}<3
101.1.27補充
臺灣師大100學年度大學甄選入學指定項目甄試試題
http://www.math.ntnu.edu.tw/down/archive.php?class=105
http://www.math.ntnu.edu.tw/down ... 6%E8%A9%A6%E4%B8%80
題目一模一樣，所以華江這份題目應該是師大教授出的
3.
將長
\overline{AB}=240 ，寬
\overline{Bc}=288 的長方形紙張對摺，讓頂點C剛好落在線段
\overline{AB} 的中點M上，如下圖所示：
已知
\overline{EF} 是摺線，求摺線
\overline{EF} 的長度。
[提示]
假設
\overline{CF}=x ，
\overline{DE}=y
△BFM,△AEM,△C'ME為直角三角形，用商高定理
105.6.5補充
105高雄餐旅附中考了一模一樣的題目
https://math.pro/db/thread-2527-1-1.html
有一邊長為1的正方形ABCD，將B點折至
\overline{CD} 間的B'點(如圖)，折痕為
\overline{PQ} ，此時A點落於A'處，
\overline{A'B'} 與
\overline{AD} 的交點為點R，則△RB'D的周長為何？
(建中通訊解題第61期)
如圖，ABCD是邊長為1的正方形，沿
\overline{PQ} 對折，使得A,B對折之後分別重合於A',B'兩點，且B'在
\overline{CD} 上，
(a)證明△RB'D的周長為2。
(b)求△QB'C的最大面積。
(97國立大里高中，
https://math.pro/db/thread-2402-1-1.html)
