各位老師好：
最近在練習題目時有幾題題目想了很久，有想法，但都還是無法完全做出來。
題目如附加檔案。(不好意思，不太會用直接在網站上敲數學式子 ><)
第2題我證明出來最後差個負號，整理不出來。
第4題想使用錯排原理去解題，但是答案相去甚遠。但又不知道錯排這個方法盲點在哪。

請各位老師有空時不吝賜教，謝謝各位老師。

1.三角形ABC，∠A的內角平分線AT交BC於T點，試證AT=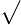ABAC−BTCT [98新港藝術高中]

2.a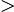b，試證：雙曲線b2x2−a2y2=a2b2互相垂直的二切線的交點必在圓x2+y2=a2−b2
[98新港藝術高中]

3.有兩射線OX，OY夾角60o，P為∠XOY內部一點，OP=10，今欲在OX上取一點A，OY上取一點B，使△PAB之周長最小，若△PAB之最小周長為t，則(A)16t17　(B)17t18　(C)18t19　(D)19t20
[98全國聯招]

4.將5個A，5個B，5個C，共15個字母排成一列，使得前5個位置不排A，中間5個位置不排B，最後五個位置不排C，排法有幾種

5.柔道擂台賽，比賽過程是：甲、乙二隊各出7名隊員按事先安排的順序出場比賽，雙方先由1號隊員出賽，負者遭淘汰；負方再派2號出場迎戰勝方的1號，L以此類推，直至一方7名隊員全被淘汰為止，另一方獲勝。所有可能出現的比賽過程的個數為[93學年度高中數學能力競賽中區(嘉義高中)　筆試(二)試題]

第一題：利用內分比性質，加上餘弦定理，就可以證明出來了。

　　　　善用餘弦定理，其實也可以證個較廣義的 Stewart's theorem，如下

　　　　對於 ABC，BC 上任取一點 T，

　　　　可以證明：AT2=BT+CTAC2BT+AB2CT−BTCT




第二題：方法同 https://math.pro/db/thread-723-1-2.html



第三題：將 P 對稱 \overrightarrow{OX}、\overrightarrow{OY} 分別得 P_1, P_2，

　　　　則 t= \overline{P_1P_2} 且 \angle P_1OP_2=120^\circ，

　　　　利用餘弦定理，可得 t^2=10^2+10^2-2\times10\times10\cos120^\circ \Rightarrow t=10\sqrt{3}.



第四題：https://math.pro/db/thread-454-1-3.html



第五題：h ttp://forum.nta.org.tw/examservice/showthread.php?t=15133　連結已失效