這題我之前有整理過,請一併準備
整数
 10931031+3
10931031+3
的末两位数是?(1993全国高中数学联合竞赛试卷)
h ttp://forum.nta.org.tw/examservice/showthread.php?t=52834 連結已失效
的"大陸全國高中數學聯合競賽.rar"
試求
 10931031+3
10931031+3
的末尾兩位數字和為。(其中:表示不超過的最大整數)
(94台中縣高中聯招)
高斯函數
 10931031+3
10931031+3
的末尾兩位數字和為?
h ttp://forum.nta.org.tw/oldphpbb2/viewtopic.php?t=20850 連結已失效
102000 被
10100+3 除,商的個位數為
a,餘數的個位數為
b,求數對
(a b)
b)?
(95中興高職,h ttp://forum.nta.org.tw/examservice/showthread.php?t=13559 連結已失效)
試證:
 102000010100+3
102000010100+3
之個位數字為3,(其中
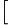 x
x
為
x 之高斯整數)。
(95高雄市聯招)
h ttp://forum.nta.org.tw/examservice/showthread.php?t=2633 連結已失效
https://artofproblemsolving.com/community/c4h234350
https://math.pro/db/thread-2125-1-1.html
試求
 10200110667+2002
10200110667+2002
的末四位數,其中
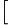 x
x
表示小於或等於
x 的最大整數。
(2002TRML團體賽,96中一中)
103彰化高中,
https://math.pro/db/thread-1890-1-1.html
111.4.24補充
試求
 10202210674+2022
10202210674+2022
的末4位數,其中
[]表不大於
x的最大整數。
(111台中一中,
https://math.pro/db/thread-3635-1-1.html)
113.5.12補充
[x]表示小於或等於
x的最大整數,則
 10202510675+2025
10202510675+2025
的末三位數為
。
(113內湖高工,
https://math.pro/db/thread-3866-1-1.html)