題目還沒釋出，分享一下我記憶中的計算題一跟二，希望有人可以記得三跟四謝謝！

F58D2E78-8E1B-4718-BA5D-5E097100E666.jpeg (321.48 KB)

2022-4-24 08:44

題目已釋出，但沒計算題

111.4.25補充
第一部分填充4答案更正為1

計算2，已知 abc=1, a,b,c 皆正，求證：

1/a^3(b+c) + 1/b^3(a+c) + 1/c^3(a+b) >= (1/a+1/b+1/c)/2

我的作法：
b^2c^2/a(b+c) + a^2c^2/b(a+c) + a^2b^2/c(a+b) >=(科西) (ab+bc+ab)^2/(2(ab+bc+ac)) =(ab+bc+ac)/2 = (1/a+1/b+1/c)/2

計算4
令 P(x^2023) +x^3Q(x^2023) + x^5R(x^2023) = (1+x+...+x^2022)S(x)
求證：S(x) 有 (x-1) 之因式

我的作法：
令 w = cos pi/2023 + i sin pi/2022
x=w, x=w^2 ,.., x=w^2022 帶入相加，可得 P(1)=0
左右同除x^3, 再一次用 x=w, x=w^2 ,.., x=w^2022 帶入相加，可得 Q(1)=0，
同理R(1)=0，因此S(1)=0，得證。

2.
假設[]為高斯記號(說明：例如[a]表示小於或等於實數a的最大整數)，請求出方程式x2−12[x]+11=0的所有解　　　。

[]表高斯符號，求解3x2−19[x]+20=0。
(105高雄餐旅大學附屬高中，https://math.pro/db/thread-2527-1-1.html)



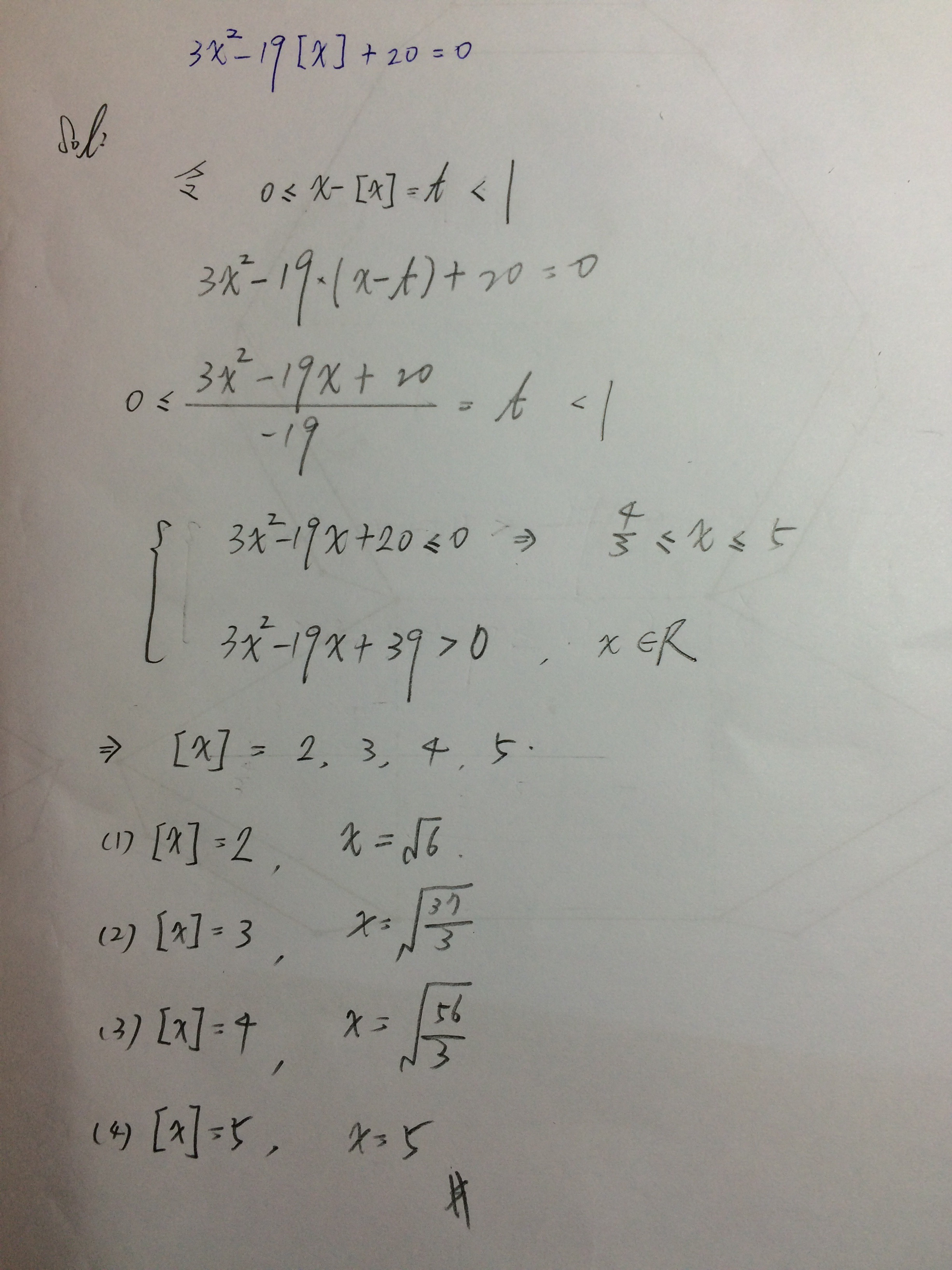
3.
設、、、為方程式x4+13x3+17x2+6x+1=0的四個根，求12+12+12+12的值為　　　。
[提示]
令1+13y+17y2+6y3+y4=0四根為1111
再用https://math.pro/db/viewthread.php?tid=1019&page=1#pid2501方法下去算

設4x3+3x2+2x+1=0三根為，則15+15+15？
(100苑裡高中，https://math.pro/db/viewthread.php?tid=1178&page=1#pid3963)

5.
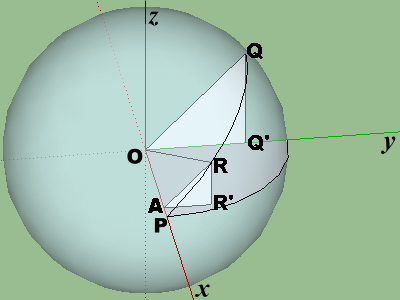
設地球為空間中一球體。今以地球球心為原點，地球半徑為單位長，建立一個直角坐標系。若地球表面上有甲、乙、丙三地，甲、乙的坐標分別為(100)及(02123) ，而丙地位於甲乙兩地之間最短的路徑上，且甲丙路徑長為乙丙路徑長的2倍，求丙地的坐標　　　。

今一單位球(半徑為1的球)球心為原點，且球面上兩點P、Q座標分別為P(100)、Q(02222) ，延著球面行進，於PQ最短路徑中取一點R，使得(PR弧長)：(QR弧長)=1：2，試求R點座標。
(99大安高工，https://math.pro/db/viewthread.php?tid=960&page=1#pid2178)


12.
桃園高中80周年慶，師生想利用8個8組成一個校運昌隆數作為紀念，經過討論後決定以88888888作為此校運昌隆數。將此校運昌隆數展開後的各位數字和令為A，再將A的各位數字和令為B，求B的各位數字和為　　　。

When 44444444 is written in decimal notation, the sum of its digits is A. Let B be the sum of the digits of A. Find the sum of the digits of B. (A and B are written in decimal notation.)
1975IMO，https://artofproblemsolving.com/ ... _Problems/Problem_4
weiye解題，https://math.pro/db/viewthread.php?tid=1387&page=1#pid6086

計算2.
已知 abc=1,a,b,c皆正，求證：\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(a+c)}+\frac{1}{c^3(a+b)}\ge \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}{2}

Let a, b, c be positive real numbers such that abc=1. Prove that \displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(a+c)}+\frac{1}{c^3(a+b)}\ge \frac{3}{2}.
1995IMO，https://artofproblemsolving.com/ ... _Problems/Problem_2

填充4
設0\le x \le \pi，求1+\sqrt{sin x}-\sqrt{x}=cos2x+2x^2的實根個數　　　。
[疑問]
應該能整理成2x^2-x^(1/2)=2(sinx)^2-(sinx)^(1/2)
由於y=2x^2-x^(1/2)嚴格遞增
解應該發生於x=sinx
此時x=0
故實根應只有一個
想請問各位老師，我的過程是否有誤？

引用:

原帖由 zerogil159 於 2022-4-24 11:53 發表
填充4
應該能整理成2x^2-x^(1/2)=2(sinx)^2-(sinx)^(1/2)
由於y=2x^2-x^(1/2)嚴格遞增
解應該發生於x=sinx
此時x=0
故實根應只有一個
想請問各位老師，我的過程是否有誤？ ...

我覺得答案可能給錯了~應該只有一個實數解
1+√ (sinx)-√ x =cos(2x)+2x²  ,
整理成2[(sinx)²-x²]+(√ (sinx)-√ x )=0
(√ (sinx)-√ x) [2√ (sinx)+2√ x+1]=0
√ (sinx)-√ x=0 =>sinx=x-------(*)
∵0≦x≦π,畫圖可知僅當x=0時
符合(*)的解  ∴所求只有一個實數解

請問老師有提試題疑義了嗎？

好的 麻煩zerogil159老師了

我正在寫，等等提出

第一部分填充4答案更正為1了

一、填充5
設地球為空間中一球體。今以地球球心為原點，地球半徑為單位長，建立一個直角坐標系。若地球表面上有甲、乙、丙三地，甲、乙的坐標分別為(1,0,0)及\displaystyle (0,\frac{1}{2},\frac{\sqrt{3}}{2})，而丙地位於甲乙兩地之間最短的路徑上，且甲丙路徑長為乙丙路徑長的2倍，求丙地的坐標　　　。
[解答]