選擇10
10.
集合12360的子集合S，其中S滿足任兩個元素的和不為7的倍數，則n(S)的最大值為
(1)6　(2)17　(3)14　(4)27　(5)28
[解答]
1~60的整數裡面分成7類
7K:8個
7K+1，7K+2，7K+3，7K+4皆9個
7K+5，7K+6皆8個
容易判斷出至少取7K+1，7K+2，7K+3 共27個可滿足題意
此時再配上7K裡面的任意一個數，即可有最大值共28個


填充11
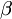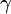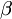
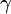
已知x3−3x+1=(x−2cos)(x−2cos)(x−2cos)，且0180，試求sin(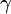−)之值=　　　。
[解答]
2cosA，2cosB，2cosC代入方程式，可得cos3A=-1/2 (B，C同理)

所以3A=120度，240度，480度
A=40度，80度，160度
再依序排列得到C=160，A=40
所求為sin120度

選擇5
5.
四個正整數a、b、c、d的乘積為8!且滿足ab+a+b=524bc+b+c=146cd+c+d=104，請問a−d=
(1)12　(2)10　(3)8　(4)6　(5)4
[解答]
ab+a+b+1=525
即(a+1)(b+1)=525
同理得(b+1)(c+1)=147
           (c+1)(d+1)=105
b+1是525和147的公因數 其中gcd(525，147)=21
發現b+1=21，c+1=7，d+1=15，a+1=25
b=20=4*5
c=6=6
d=14=2*7
a=24=8*3
abcd剛好為8!
故所求a-d=10

請教填充14.19.20.25.26.28

填充第 14 題
設a、b、c、x、y、z均為實數，若a2+b2+c2=1，x2+y2+z2=4，則a+bx+y3b+cy+z4a+cx+z3的最大值為　　　。
[解答]
參考 http://www.shiner.idv.tw/teachers/viewtopic.php?p=27713#p27713

第19題
設兩複數z1=cos3+isin3，z2=cos4+isin4，若z3=z1z2，z4=z2z1且a為實數，則a−z3+a−z4之最小值為　　　。
[解答]
  z3=cos712+isin712  z4=cos112+isin112  
它們是高斯平面單位圓上的兩點
所求即x 軸上一點，到此兩點距離和之最小值

第20題
大於(3+2)6 的最小整數為　　　。
[解答]
考慮3+26+3−26 
而3−26 很接近0

第25題
設為方程式log107x=−x+3的實根，為方程式107x=−x+3的實根。則(log107)+107之值為　　　。
[提示]
畫出y=log107x、y=107x、y=−x+3之圖形
前兩者對稱於y=x
……


第26題
設a=323−5+323+5 ，則a6−9a2−18a−4之值為　　　。
[提示]
a3=3+3a
……


第28題
試求最接近於100010000n=31n2−4 之整數為三位數abc，則a+b+c=　　　。
[提示]
1n2−4=411n−2−1n+2 ，再相消

感謝各位這份練習過