感激，誤會可大了。如果考場犯了這種錯誤，一定噢死。原來重頭到尾只有投擲兩次。那這題目不難。謝謝

那乾脆把這美麗的誤會繼續玩下去

改成：一直擲，過程中，會連續出現兩次正面的機率。

直覺上的答案應該是 1，計算如下，以 A, B, C 三數代表，由 A, B, C 硬幣開始擲會連續出現兩次的機率

則有以下遞迴關係

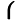
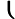
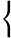
ABC=41+43(21B+21C)=9100+91100(21A+21C)=925+2516(21A+21B)

其中，若由 A 開始，兩次內，有可能連續二次正面，亦有可能出現反面後改擲 B 或 C。

解聯立方程式可得 A=B=C=1，故在此誤會情況下，所求 3A+B+C=1

話說，這類的問題，應該是有機會用 Borel-Cantelli Lemma 去處理，說它的補事件的機率為 0

填充題第九題

A=2503100
(1)logA=100log3−50log2=10004771−5003010=3266
所以A為33位數

(2)2503100550550=10503100550
31005100乘完後，小數點往左移50位。

(3)33+50=83

獻醜

計算題第一題，錯誤的原因可以這樣解釋嗎？學生那樣假設是空間中直線的參數式。。題目x+y+z=1是空間中的平面方程式。正確的解法是用柯西不等式。。。

[ 本帖最後由 shingjay176 於 2013-5-6 02:50 PM 編輯 ]

引用:

原帖由 shingjay176 於 2013-5-6 02:47 PM 發表
計算題第一題，錯誤的原因可以這樣解釋嗎？學生那樣假設是空間中直線的參數式。。題目x+y+z=1是空間中的平面方程式。正確的解法是用柯西不等式。。。 ...

我也是這樣想耶，學生假設的只是包含於空間平面上的某一條直線而已...還需要舉反例嗎（在平面上但不再學生舉的線上）？還是？

計算題第四題第一小題。我發表一下自己的看法

也來一點個人的想法：那個證明手法，每次看完之後就忘了，到底有幾次...至少也有5-6 次以上吧。

所以只好用證明 n 個數的算幾的那招方法來證廣義柯西：多用幾次柯西不等式，可以先做出 n 為 2 的冪次的結果。

當 n 不是 2 的冪次時，用幾何平均把它補到 2kn 個，即令 a=na1a2an , b=nb1b2bn 。

這樣的 (a+b) 要補 2k−n 個，再利用 2k 的結果，即得

nj=1(aj+bj)(a+b)2k−nnnj=1aja2k−n+nnj=1bjb2k−n2k 

而右式中，因 ab 分別為 ajbj 的幾何平均，故右式 =(a+b)2k

再與左式相約，即得 nj=1(aj+bj)(a+b)n ，開 n 次方，即得證之。

就是要這樣討論，才能擦出火花。更多想法才可以消化吸收後。變成自己的解題技巧。

這兩種解法也太強大!!!
比我的好多了，我的解法很難寫......
我是先除以 na1a2an  ，

並令  aibi=ri

變成  n(1+r1)(1+r2)(1+rn)1+nr1r2rn 

這就跟之前有人PO過的這個年度學科能力競賽台北市複賽其中一題一樣了。
接著兩邊n次方後用二項式定理和算幾不等式完成。
補充，據說北市複賽講評時，教授說此題用廣義柯西不得分。