就小弟的印象記憶法,僅供大家參考和討論(題號無法清楚背誦,很抱歉!)
1. 袋中有2個白球和4個紅球,朱哥手中有1個白球,規則為從袋中取一球,在將手中的球放入袋中。每次取球機率都相等,且第三次取出為白球,求第六次取出白球的機率為何??
2. 甲乙丙三人打靶的機率為
 、
、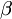 、
、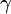
,且


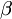

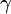
。三個人都沒打中靶的機率為
415,洽中一發的機率為
715,洽中兩發的機率為
730,且都是獨立事件,求
 、
、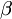 、
、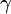
=??
3. 若a、b、c、d、e為
X5−2X4+3X3−4X2+5X−6的五個根,請求
11−a+11−b+11−c+11−d+11−e=??
4.請證明
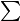 nK=1K4
nK=1K4
5.若
Z為一個複數,且
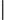 Z
Z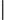
 21
21,請求出
Arg(1+Z)=??
6.解出
cos4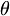 =sin
=sin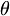
,且
0
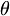
 2
2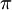
7.證明
Xn+1+n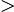 X(n+1)
X(n+1)
8.計算出
y2=x(x−4)2的面積=??
9.有一個橢圓為
a2x2+y2b2=1,且
a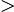 b
b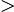 0
0,若在橢圓上找一個點為成一個梯形,且下底為長軸,試問此梯形面積最大值為=??
如果有任何記錯題目的部分,還希望各位老師多多指教!!
自己想要問第5題和第8題!多謝各位老師
(第八題已修改!多謝!)
【註:weiye 將八神庵所提供之官方公告版試題附加於附件。101.07.04】