引用:

原帖由 larson 於 2012-7-1 01:31 AM 發表
x2+y2=z2到底是什麼？我也看不出meifang 哪裏有算錯？

你先固定 z 值，那它就是一個圓
所以隨著 z 值的改變，此圓的半徑也跟著改變
同時此圓在 z 軸的位置也著都變
所以所有圓疊起來，就成了 cone


(圖片轉貼自：Theory Of Relativity)
圖片中space，即xy平面，time軸即為z軸

引用:

原帖由 meifang 於 2012-6-26 03:51 PM 發表 
第3題 我算超多遍 外加GeoGebra畫圖 長軸長為2 不知到哪裡出了問題
這是我的計算過程

z=21(1−x−y) 帶入x2+y2=z2 整理後得到
3x2−2xy+3y2+2x+2y−1=0
分別對x、y偏微分後=0
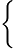3x−y=−1 −x+3y=−1 
中心點為−21−21
平移後得到
3x2−2xy+3y2−2=0
再算出3 −1−13 的eigenvalues 為4和2
因為只要問長軸長 所以先不考慮順序 得到旋轉後的橢圓為
4x2+2y2−2=0
所以長軸長為2
可以幫我看看有哪裡算錯了嗎? 謝謝

z=21(1−x−y) 代入x2+y2=z2所得到的3x2−2xy+3y2+2x+2y−1=0是在xy平面上的橢圓
算出來的長軸長AB=2，所以前面一心老師才會加上兩平面夾角的餘弦值，算出正確的長軸長AB=6 

101木柵高工第三題.gif (78.3 KB)

2012-7-3 14:01

當初用SketchUp畫圖時還想到一種方法，這在考場應該想不到
平面x+y+2z=1交三個座標軸於P(100)、Q(010)、R(0021)
將全部的圖形沿著z軸旋轉45o，讓OM變成新的y軸，x軸伸出螢幕外
此時M點坐標為(220) ，R點坐標為(021)
利用RM的直線方程式和圓錐交於A、B兩點，進而求出橢圓的長軸長

101木柵高工第三題另解.gif (24.45 KB)

2012-7-3 14:01

謝謝樓上的兩位老師 原來我只是帶入而已 卻不知不覺做了投影 果然還是要考慮圖形

在平面 ABC 過 A 作 AB 的垂線交 BC 於 P ；
在平面 ABD 過 A 作 AB 的垂線交 BD 於 Q ；
那麼 \Delta BPQ 是正三角形。
不妨假設 BP=BQ=PQ=1 ，
那麼 \displaystyle AP=AQ=\sin36^o
\displaystyle \cos{\angle{PAQ}}=\frac{2\sin^2 36^o-1}{2\sin^2 36^o}=\frac{-\cos72^o}{1-\cos72^o}
\displaystyle =-\frac{\sqrt{5}-1}{5-\sqrt{5}}=-\frac{1}{\sqrt{5}}

還記得大二修陳創義老師的幾何學的時候，老師要我們作模型，以及要我們報告；
我就把這五個正多面體的兩面角、內外接球半徑和邊長的比例、中心角等等的數據算出來，
雖然當時不是這樣算，而是利用趙文敏老師在他的數論淺談一書中提過的黃金矩形的性質來算，
但是覺得有所獲得，也發現一件有趣的結果。找機會考考學生好了。

引用:

原帖由 老王 於 2012-7-3 10:44 PM 發表
在平面 ABC 過 A 作 AB 的垂線交 BC 於 P ；
在平面 ABD 過 A 作 AB 的垂線交 BD 於 Q ；
那麼 \Delta BPQ 是正三角形。
不妨假設 BP=BQ=PQ=1   ...

不懂為什麼三角形BPQ是正三角形？

因為三角形BCD是正三角形，
所以角PBQ=60度
又BP=BQ，所以BPQ是正三角形

引用:

原帖由 casanova 於 2013-4-24 11:15 PM 發表

不懂為什麼三角形BPQ是正三角形？

另解