引用:

原帖由 meifang 於 2012-6-26 09:28 PM 發表
我想問一下第8題 應該不會很難 但是我不會
第9題 完全不知怎麼下手

#8
令t=x+1/x
則x^2+(1/x)^2 =t^2-2
原式=>
t^2-2 -2t-1=0
t^2-2t-3=0
(t-3)(t+1)=0
t=3或-1
(i)當t=3時
x+1/x =3
x^2-3x+1=0有實數解
兩根和=3
(ii)當t=-1時
x+1/x=-1
x^2+x+1=0沒有實數解

我的想法是長期之後
從3R1W中取3顆給甲袋
又從甲袋裡的紅球3顆取一顆
P(A)=43C31C=43
不知道這樣可不可以，也順便請問大家的看法！！

個人認為第五題題目有問題，因為農曆的算法，月日的部分跟國曆不同，
還有閏月的情形，這已不是現在熟習國曆的我們所能了解的!!

填充 8. 令 t=x+x1，係數對稱時，常用的招式

填充 9. 需要的圖，去wiki 看一下好了

一個頂點有三個正三角形，而這五個正三角形如果拿掉這個中心的頂點，就變成正五邊形

相鄰兩三角形，作兩條高垂直共邊，其長為 23a , 其中 a 正三角形之邊長

而此相鄰兩三角形，不在不共邊的兩點即前所說正五邊形上的不相鄰兩點，其距離為 25+1a 

以此 23a23a25+1a  三邊為三角形的等腰三角形之頂角，即為兩面角

由餘弦定理可得  cos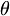=24343+43−46+25=−35 

算到這，我們應該留個習題，正十二面體的兩面角是的餘弦值是多少

P.S. 其實是小弟眼殘，先算了 12 的發現和答案不一樣，之後才發現是 20 的正三角

[ 本帖最後由 tsusy 於 2012-6-26 10:26 PM 編輯 ]

引用:

原帖由 tsusy 於 2012-6-26 10:20 PM 發表
填充 8. 令 t=x+x1，係數對稱時，常用的招式

填充 9. 需要的圖，去wiki 看一下好了

一個頂點有三個正三角形，而這五個正三角形如果拿掉這個中心的頂點，就變成正五邊形

相鄰兩三角形，作兩條高垂直共邊，其長為  ...

我考試的時候就眼殘，看成12面體，很開心的直接寫了cos值為1/2~希望這題習題改成這樣有對!!

這位同學，你算錯了

sorry，老王老師，我再來好好做一次，圖形畫錯了，一步錯，步步錯!!!!-_______-////

引用:

原帖由 meifang 於 2012-6-26 03:51 PM 發表
第3題 我算超多遍 外加GeoGebra畫圖 長軸長為2 不知到哪裡出了問題
這是我的計算過程

z=21(1−x−y) 帶入x2+y2=z2 整理後得到
3x2−2xy+3y2+2x+2y−1=0
分別對x、y偏微分後=0 ...

x2+y2=z2到底是什麼？我也看不出meifang 哪裏有算錯？

想請教十二面體兩面角算法,
我練習算,但是算不出正解><

我找了正十二面體的圖


只能推到要計算 一個四面體ABCD 其中AB=AC=AD=1  BC=CD=BD=21+5 
ABC與  ACD的夾角 可是我還是不會算

[ 本帖最後由 meifang 於 2012-7-3 12:24 AM 編輯 ]