引用:

原帖由 shiauy 於 2012-4-27 01:29 PM 發表
分子：H42
看成是y+z=4的非負整數解

分母：H63
看成是x+y+z=6的非負整數解

請問這跟f大的答案差異
造成出入的原因為何？

有出入的原因是因為你把球視為一樣 ^^

個人認為，真正的問題，在於 #3 所給之問題題意不明

「將6個相同的球，放進甲、乙、丙等3個不同的箱子中，每箱球數不限，則甲箱恰得2球的機率為何？」

敘述中，並不任何隨機、機率的敘述，才會造成各個的解讀的不同

舉例來說：丟一枚公正的硬幣，正反出現的機率皆為 21

就是公正二字，告訴了我們隨機、機率的訊息。

如果，今天是丟一枚不公正的硬幣，那又有誰曉得正反的機率是多少呢？

但實際上，在經過做題目的制約作用後，往往我們會習慣，談硬幣、骰子，就是公正、正常的硬幣、骰子

而古典機率中，使用事件集合的元素個數/樣本空間的元素個數

回到硬幣的問題，我們所知「公正」的事是每個硬幣出現正反的機會一樣

而樣本空間本身，是一種人為的定法，我們兩個人可以各自定義不同的樣本空間，

但只要這兩個樣本空間是公平，那計算的機率就相同。

例如在撲克牌的問題，5 張牌，計算 2 pairs 或 三條等的機率

有人覺得，要算機率，不管三七二十一 ，五張視為不一樣，算排列數，算完再除以分母 P552

實際上，以前讀書時，某段時間，自己就是這樣。

但實際上，拿到任五張的機率一樣，所以用組合算，算完再除以分母 C552，答案也是相同。

老實說，我不太懂TSUSY老師的意思 ^^!!

那TSUSY老師覺得那一題的題目該如何改比較不要造成誤會？

應該這麼說，為什麼有的題目視為相同或相異的結果會一樣，

原因是視為相同時，每一情況在樣本空間出現的機會一樣，
視為相異時，若剛好每一情況的排列數是相同的話，那麼它們在樣本空間出現的機會也會剛好一樣，
所以視為相同與相異的結果都一樣，就如同你舉的撲克牌的例子，

但有的題目將物品視為相同時，每一情況在樣本空間出現的機會並不一樣，

所以不能直接套用古典機率，那會違背古典機率的前提，

通常這個都是題目中的物品是「實際的物體」時才會發生的情形。

[ 本帖最後由 poemghost 於 2012-5-10 09:04 PM 編輯 ]

也許是我的回答，模糊了焦點，其實我想說的是有沒有自明的隨機性

而當題目沒有自明隨機性的時候，自然會產生誤會

而自明的隨機性，來自哪了？通常是應該是來自實際操作的經驗，這樣說應該還是很模糊，而且也許不對，

舉例來說：箱子中有 6 紅球 5 黃球 3 白球，任取一球，是紅色的機率是 611

問題可以繼續延伸，如問取後不放回，紅球先取完的機率是多？

這個問題中，隱含自明的是：每次取球箱中任一顆球被取到的機率一樣

再一個例子，據說是台大某年的微積分考題

在圓上任取一弦，求弦長的期望值

據說，當時學生算出來多種不同的答案，原因何在？

就是我所說的，缺少自明的「隨機性」，所以不同的人用不同的抽樣方式計算。

如可能這樣計算，選定某一方向的弦算就好了，反正方向對稱，然以架坐標(設半徑 1)

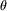列出這樣的 21−121−x2dx    或是 02sind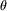 

不知道這個例子，是否能表達出我要說的事了

另外，突然想起來以前考試的時代，也許那時候還沒被制約...

不知道大家是否也有這樣經驗，題目明明是問機率，但敘述中卻是一件確切的事，只是不知道結果而已(好像是一個普查問題...本來抽樣的平均值有隨機性，但一普查，就變母群體的真平均值，是固定的數，沒有隨機性)

然後，在答案欄裡填上 1 或 0，但顯然答案一定不是這樣，之後再跑去找老師說題目敘述的疑義

所以，回到 # 3 的問題，個人的看法是，不是隨機的東西，就不應該亂問機率才是

如果真的要問，可能改成「將6個相同的球，任意放進甲、乙、丙 3個不同的箱子中，每球放入每箱的機率相同，並且互不影響。則甲箱恰得2球的機率為何？」

本來應該是獨立的說法，但用獨立事件敘述，好像有點麻煩 (其實是想用獨立變數，但高中沒有...)

再翻了一下手邊全華第二冊的課本，在習題 3-1 有一個這樣問題，其敘述如下：

將 6 個相同的球，放入甲、乙、丙三個不同的箱子中，S 表甲、乙、丙三箱分別放置球數之樣空本空間，A 表甲箱球數大於乙箱球數之事件，B 表甲、丙兩箱球數和為 5 的事件，
1. 試求 n(S)。
2. 以列舉法表 A 與 B 的積事件。

附帶一提，3-1 的標題是「樣本空間與事件」，之後這個問題在第三章的就沒有再出現過了。

也許編者也有注意到相同的事，所以之後第三章都沒有問這個機率的題目，並把它放在古典機率之前，所以只是單純的樣本空間，並不一定公平

[ 本帖最後由 tsusy 於 2014-5-29 08:38 AM 編輯 ]

不知道為什麼，小弟突然聯想到了張海潮教授寫的一篇《審書趣談》

http://mathcenter.ck.tp.edu.tw/R ... 1-a8c4-4dcaa163d2a3

要點連結中的＂詳全文＂喔！

袋中有三黑四白 自袋中隨機抽取一球 取後不放回 有一種色球取完就停止  全部洽取五球的機率

解1
慮第五顆球是黑球或白球兩種情況
1.第五顆是黑球，前四顆是2黑2白，所以共有4! / (2!2!)=6種
2.第五顆是白球，前四顆是1黑3白，所以共有4!/3!=4種
[ (3*2*1*4*3) / (7*6*5*4*3) ] *6 + [ (4*3*2*1*3) / (7*6*5*4*3) ] *4 = 2/7


解2
(1) 第 5 球是黑球，前 4 球 2 黑 2 白：4! / (2!2!) = 6
(2) 第 5 球是白球，前 4 球 1 黑 3 白：4! / 3! = 4
所求 = (6 + 4) / [7! / (3!4!)]

Q
請問此題的樣本空間是    7*6*5*4*3  還是  7! / (3!4!)

還有像這種有一樣的色球 在考慮樣本空間  到底是將每個同色球視為相異還是視為相同
如三黑四白 逐一取球  樣本空間是  7!  還是   7!/3!4!  如何跟學生解釋

袋子中有三顆黑球  四顆白球  每次取出一球取後不放回  而在有一種色球被取完時就停止 則全部取五球的機率是

解1
慮第五顆球是黑球或白球兩種情況
1.第五顆是黑球，前四顆是2黑2白，所以共有4! / (2!2!)=6種
2.第五顆是白球，前四顆是1黑3白，所以共有4!/3!=4種
[ (3*2*1*4*3) / (7*6*5*4*3) ] *6 + [ (4*3*2*1*3) / (7*6*5*4*3) ] *4 = 2/7
解2
(1) 第 5 球是黑球，前 4 球 2 黑 2 白：4! / (2!2!) = 6
(2) 第 5 球是白球，前 4 球 1 黑 3 白：4! / 3! = 4
所求 = (6 + 4) / [7! / (3!4!)]

請問這個問題的樣本空間是  7*6*5*4*3  還是 7! / (3!4!)
這類逐一取球問題在考慮時 樣本空間到底要怎麼考慮  是要本同色球看成相異 還是相同(不盡相異物排列)  
如何跟學生說

這問題延續本討論串，因此合併主題。

在這個問題裡，當成相同球與相異球時，所列樣本空間雖然不同，但是兩個樣本空間
裡的樣本點出現的機會是均等，計算起來是事都可以的，另外注意一件事情，兩種計算
方式分子與分母差別在於是否同乘3!4!，也就是說每一個當成相同物的樣本點會對應
對應4!3!個當成相異物的樣本點。
    跟學生解釋時，我會跟學生說，現在你是閉著眼睛取球，沒有球相不相同問題。
但是要強調的事，依照古典機率的定義，所列出的樣本空間裡的樣本點出現的機會
需均等。

先前在國中教甄，99年南區遇到一個機率問題：

36.(Ｂ)   將5個相同的球分給三個小朋友，則其中有一個小朋友沒有分到球的機率是多少？
　         (A)2/7  (B)4/7  (C)5/21  (D)7/21

　在友板與人討論，有兩種不同的說法，想向大家請教一下哪一種才是正確的想法：
　(a)  把相同的球編號視為相異物，則所有的可能有3^5=243種
　　　一個小朋友沒有拿到球：球全部分給另外兩個小朋友　3*(2^5-2)=90
          因此機率為90/243＝10/27  .....沒有正確答案

　(b)  這題根本不需要將球編號,一看就要用重複組合方式
          假設第一位得x顆,第二位得y顆,第三位得z顆,x+y+z=5
          S:樣本空間,A:其中有一個人沒有得到球的事件
          n(S)=H(3,5)=C(7,5)=7*6/2=21
          n(A)=C(3,1)*[H(2,5)-2]=3*[C(6,5)-2]=3*4=12
          (先選沒得到球的人,剩下兩人分5球,要扣掉(0,5) ,(5,0) 情況)
          所求p(A)=n(A)/n(S)=12/21=4/7
          A包含在S內,並沒有矛盾,答案也沒有錯~
　　   您將球編號去分組作,基本上方向就錯了~　　　　　　此想法由Ellipse老師提供，原文轉述，一開始沒有標註是我的疏忽，非常抱歉！

兩個說法在友版有非常激烈的爭論，這裡討論的人比較多，想知道更多人的想法，謝謝！

[ 本帖最後由 farewell324 於 2014-5-23 06:50 PM 編輯 ]