不失一般性,設 \(\triangle ABC\) 中,\(\angle BAC\geq 120^\circ\),
\(E\) 為 \(\triangle ABC\) 內部異於 \(A\) 之點,
如下圖,可做 \(\triangle ABD, \triangle AEF\) 為正三角形,

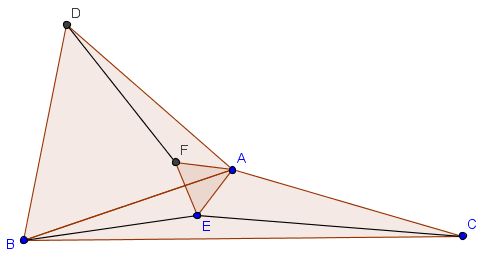
可知 \(\triangle ABE\sim \triangle ADF\),
因此 \(\overline{EA}+\overline{EB}+\overline{EC}=\overline{DF}+\overline{FE}+\overline{EC}\)
連接 \(\overline{DE}, \overline{DC}\)

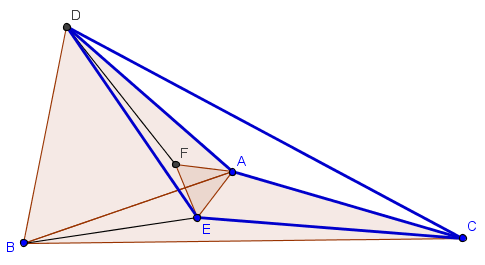
可知 \(\overline{DF}+\overline{FE}+\overline{EC}\geq \overline{DE}+\overline{EC}\)
因為 \(\angle DAB+\angle BAC\geq 60^\circ+120^\circ=180^\circ\)
所以 \(A,E\) 皆在直線 \(CD\) 的同側,且 \(A\) 為 \(\triangle CDE\) 內部之點,
可知 \(\overline{DE}+\overline{EC}\geq\overline{DA}+\overline{AC}\)
故,
\(\triangle ABC\mbox{內部一點} E \mbox{到} A,B,C \mbox{三點頂的距離}=\overline{EA}+\overline{EB}+\overline{EC}\)
\(=\overline{DF}+\overline{FE}+\overline{EC}\)
\(\geq \overline{DE}+\overline{EC}\)
\(\geq\overline{DA}+\overline{AC}\)
\(\geq\overline{BA}+\overline{AC}\)
\(=E \mbox{到} A,B,C \mbox{三點頂的距離}\)