很多題目非常適合教甄出題，我將找得到出處的題目列出來，讓各位網友可以循著連結找到答案

已知在△ABC內一點分別與各頂點連線延長至對邊，將△ABC分成六塊區域，其中四塊區域面積值如下圖所示，求△ABC的整個面積。
(98高中數學能力競賽台南區)
(1985AIME第6題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=1985)


設n為正整數，如果恰有一正整數k滿足不等式815nn+k713，試求滿足上述條件的最大值？
(98高中數學能力競賽台南區)
http://www.math.nuk.edu.tw/senpengeu/HighSchool/2000_Taiwan_High_KaohsiungCity_01.pdf
(88高中數學能力競賽高雄區)
(1987AIME第8題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=1987)


直角三角形ABC中，∠C=90o，P為△ABC內部一點，使得∠APB=∠APC=∠CPB，且PA=8，PC=6(如下圖所示)，試求PB
(98高中數學能力競賽台南區)
(1987AIME第9題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=1987)

已知xk1，k=1,2,...,n且知x1+x2++xn=97+x1+x2++xn，試確定n的最小值。
(98高中數學能力競賽台北市口試試題)
(1988AIME第4題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=1988)

已知x,y,z皆為正實數，且滿足方程組log10(2000xy)=4+log10xlog10ylog10(2yz)=1+log10ylog10zlog10(zx)=log10zlog10x，則x+y+z的值為何？
(98高中數學能力競賽高雄區)
(2000AIME，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=2000)


令a,b,c為三個正實數且滿足a+b1=4，b+c1=1，c+a1=37。求abc= ？
(2000AMC12第20題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=44&year=2000)
(2000AIME第7題，http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=45&year=2000)

試求方程式2a+2b+2c+2d=10625的整數解(a,b,c,d)，其中a>b>c>d。
(98高中數學能力競賽高雄區)
求滿足w>x>y>z條件的方程式2w+2x+2y+2z=128841其所有整數解。
(建中通訊解題第45期)


設1−21+31−41++151−152=pq，其中p，q為互質的正整數。試證：q可被79整除。
(98高中數學能力競賽第一區筆試一)
http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&t=1251


設M,A,T,H分別代表不同的阿拉伯數字。若MA與TA這兩個二位數的乘積滿足MA與TA這兩個二位數的乘積滿足MA乘TA等於HHH，則M+A+T+H =______。ans:21

已知在邊長為1的正方形內可以作出內接正三角形，那麼這些正三角形的面積之最大值為_____. ans:sec^2(15度)
thepiano解題，http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&p=7927

101.11.11補充
設a與b為實數且a0，已知a+loga=8且b+10b=8，則a+b之值為？
(98高中數學能力競賽　台北市筆試二)

若是31x+3x=8的一個根，是x+log3(x+1)=24的一個根，+=？
(100高中數學能力競賽　臺北市筆試二試題，https://math.pro/db/thread-1349-1-2.html)

108.5.11補充
若實數xyz滿足x+y+z=4x2+y2+z2=10x3+y3+z3=22，則xyz=　　　。
(98高中數學能力競賽 第四區(新竹高中)
(108板橋高中，https://math.pro/db/thread-3125-1-1.html)

在一正方形球枱中，一球從底邊中點A處出發，往右邊界83處碰撞後反射(如圖)，假設在完全彈性碰撞下，球在第一次回到A點之前共反射　　　次。
(98高中數學能力競賽 第二區(新店高中))

在一正方形球枱中，一球從底邊中點A處出發，往右邊界43處碰撞後反射(如圖)，假設在完全彈性碰撞下，球在第一次回到A點之前共反射　　　次。
(108板橋高中，https://math.pro/db/thread-3125-1-1.html)


設函數f：(0,1)\to R定義為
f(x)=\cases{\displaystyle x,x \notin Q \cr \frac{2p+1}{2q},x=\frac{p}{q},(p,q)=1,0<p<q,p,q \in N}
求f(x)在區間 \displaystyle \left(\frac{1}{3},\frac{3}{7}\right) 上的最大值？
(98高中數學能力競賽 第八區(高屏區))

設函數f：(0,1)\to R定義為f(x)=\cases{x,x \notin Q \cr \frac{p+1}{q},x=\frac{q}{p}},其中p,q \in N且p,q互質。則f(x)在區間\left(\frac{3}{7},\frac{9}{10} \right)上的最大值為　　　。
(108板橋高中，https://math.pro/db/thread-3125-1-1.html)

110.8.15補充
設\Delta ABC為等腰直角三角形，依下列兩種方式可作出其內接正方形如圖(I)、(II)所示。已知圖(I)的正方形面積為625，則圖(II)的正方形面積為。

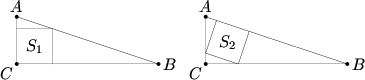
(1987AIME第15題，https://artofproblemsolving.com/ ... Problems/Problem_15)

設正實數數列 \{ a_n \} 滿足 \sqrt{a_n a_{n-2}}-\sqrt{a_{n-1}a_{n-2}}=2a_{n-1} (n≧3)，且 a_1=a_2=1 試求 a_n 。
(98高中數學能力競賽高雄區，1993大陸高中數學聯賽)


將九塊大小不等的正方形拼成一塊長方形，如下圖所示：其中黑色正方形的邊長為1，而x與y代表所在正方形的邊長。
(1)求x與y的值　　(2)求長方形的長與寬
(98高中數學能力競賽第一區筆試一)
設A與B是數線上兩個點，它們的座標分別為-1與4，如下圖所示。已知P是數線上的動點，而且滿足P到A點及P到B點的距離乘積小於6，即 \overline{PA}× \overline{PB}<6 ，求動點P的所有可能範圍是。
(98高中數學能力競賽第一區筆試二)
以上兩題是97台北縣高中聯招考題