填充4
已知m、n為正整數且m27n2，求7n2−m2的最小值　　　。
[解答]
應該還有其它更適當的解釋方法！
因為7n2  −m2  0取m=n−2，7n2  −(n−2)2  =6n2  +4n+414取m=n−1，7n2  −(n−1)2  =6n2  +2n−17取m=n，7n2  −n2  =6n2  6取m=n+1，7n2  −(n+1)2  =6n2  −2n−13取m=n+2，7n2  −(n+2)2  =6n2  −4n−412

填充6
請問滿足x1+y1=166的正整數解共有　　　組。
[解答]
H212  H212  =169

填充10
今有16枝相同的筆要全部分給A、B、C、D四人，每人至少分得一枝，若僅考慮四人所獲得筆的數量，則共有　　　種分筆的方式使得A獲得的數量大於B獲得的數量。
[解答]
2H412  −(H02  +H22  ++H212)=203

填充13
圓C的圓心為(a1)，且半徑為1，作圓C的兩條切線L1、L2，已知L1⊥L2，且L1、L2和x軸的交點分別為(−20)、(20)，求a的值為　　　。
[解答]
https://math.pro/db/thread-2632-1-1.html

填充14
設a、b、c為正實數，且a+b+c=1，求a2+b2+b2+c2+c2+a2 之最小值為　　　。
[解答]
  a2  +b2  +b2  +c2  +c2  +a2    33a2  +b2  b2  +c2  c2  +a2  332ab  2bc  2ca=32  3abc又a+b+c33abc兩式相除即最小值為2，等號成立於a=b=c=13

填充16
對於每一正整數n，f(n)+f(n+3)=n^2恆成立，若f(93)=93，求f(30)=　　　。
[解答]
\begin{array}{l} f(93) + f(30) = 90^2  - 87^2  + 84^2  - 81^2  + ... - 33^2  + 30^2  = 4590 \\ f(30) = 4497 \\ \end{array}

填充18
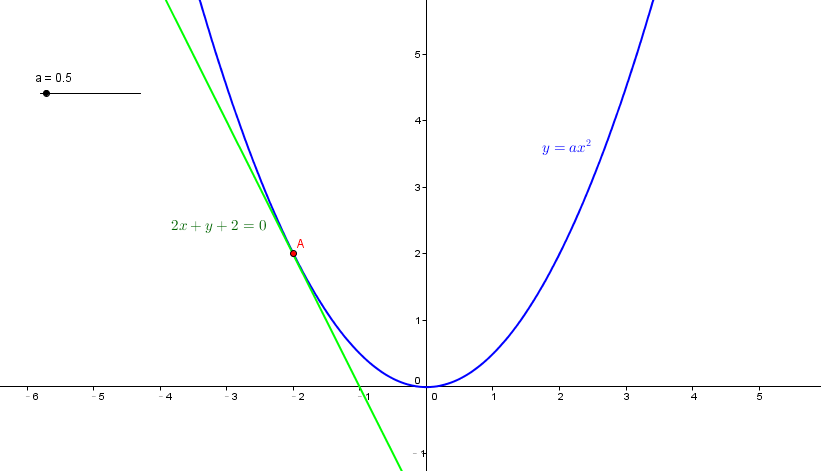
已知2x+y+2=0，試求\displaystyle log_2 \frac{y}{x^2}的最大值為　　　。
[解答]
\left\{ \begin{array}{l} 令 y = ax^2  \\ 2x + y + 2 = 0 \\ \end{array} \right. 當相切時有最大值，此時a=1/2

小弟不才，想請教thepiano大大第七題的解題構思是如何引入的呢？

感謝thepiano老師長期的熱心回覆並分享解法，小弟受到許多的幫助！感恩~~

已編輯！