想請問一下

13和17

謝謝

想通了!

謝謝

補充想通後的解法 真得很感謝thepiano大

第17題
17.
給定一個正整數N定義f(N;x)=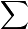ni=0aixi ，
其中a0為N的個位數字，a1為N的十位數字...，an為N的最高位數
例如：f(3456;x)=6+5x+4x2+3x3，而f(3456;1)=6+51+412+313=18
若M=1234567891011121320142015
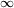令b1=f(M;2)，bj+1=f(bj;2)其中j=1234，試求limjbj=　　　。
[解答]
先舉個簡單例子 如f(abcd;2)

f(abcd;2)=d+c*2+b*2^2+a*2^3

原本abcd可表示成 d+c*10+b*10^2+a*10^3

則 abcd-f(abcd;2) 會是8的倍數 即 abcd=f(abcd;2) (mod 8)

因此 M=b(1)=b(2)=....=b(n) (mod 8)

當n夠大時 b(n)會是個位數

M (mod 8) = 7

7+8=15 & 7-8=-1 非個位數 所以只有一解7