引用:

原帖由 阿光 於 2012-6-14 03:14 PM 發表
想請教填充5,謝謝

5.
如右圖表示電路，而每個開關可使電流暢通的機率為\(p\)，且彼此不互相影響，則電流由\(L\)到\(R\)暢通的機率為何？
[解答]
分成3號開關的開與否
可以分成附件的圖來討論
3號是通的，如上圖
\(p{(1 - {(1 - p)^2})^2}\)
3號是不通的，如下圖
\((1 - p)(1 - {(1 - {p^2})^2})\)
加起來就是答案

6.
每個人都有兩隻手，在亂點鴛鴦譜的活動中，每隻手都有一個編號，隨機抽選 2 個號碼配對牽手，每人的一隻手都恰與另一隻手(可能是自己或他人的手)握住，相連在一起的人圍成一個圓圈。可能有：一人自成一圈，有 2 人牽成一圈，有 3 人牽成一圈，……。假設\(E_n\)代表\(n\)個人所結圓圈數的期望值，
(1)求\(E_1\)的值。　(2)求第一次抽選的2個號碼是同一人之機率　(3)求\(E_n-E_{n−1}=\)？　(4)求\(E_4\)的值。
[解答]
請參考許志農教授「戲說數學」
連結已失效h ttp://www.lungteng.com.tw/LungTengNet/HtmlMemberArea/publish/Math/017/01%E6%88%B2%E8%AA%AA%E6%95%B8%E5%AD%B8%E5%BA%8F.doc數學與猜想----數學期望值

引用:

原帖由 matric0830 於 2012-6-14 05:23 PM 發表
請問第14題如何證明？

如果你手邊沒有高中課本可以翻閱
google會是你的好朋友

15.
設\(P(x_1,y_1,z_1)\)、\(Q(x_2,y_2,z_2)\)，若\(ax_1+by_1+cz_1+d>0\)且\(ax_2+by_2+cz_2+d<0\)，試證明\(P\)、\(Q\)兩點必在平面\(E\)：\(ax+by+cz+d=0\)之兩側。
[解答]
P、Q點到在平面E上投影點分別為P',Q'
向量\( \displaystyle PP'=\left( - a\frac{{a{x_1} + b{y_1} + c{z_1} + d}}{{{a^2} + {b^2} + {c^2}}}, - b\frac{{a{x_1} + b{y_1} + c{z_1} + d}}{{{a^2} + {b^2} + {c^2}}}, - c\frac{{a{x_1} + b{y_1} + c{z_1} + d}}{{{a^2} + {b^2} + {c^2}}} \right) \)
向量\( \displaystyle QQ'=\left( - a\frac{{a{x_2} + b{y_2} + c{z_2} + d}}{{{a^2} + {b^2} + {c^2}}}, - b\frac{{a{x_2} + b{y_2} + c{z_2} + d}}{{{a^2} + {b^2} + {c^2}}}, - c\frac{{a{x_2} + b{y_2} + c{z_2} + d}}{{{a^2} + {b^2} + {c^2}}} \right) \)
由題目所給條件可知，向量PP'=k倍的向量QQ'，其中k為負值，故兩向量為反向
即PQ異側

4.
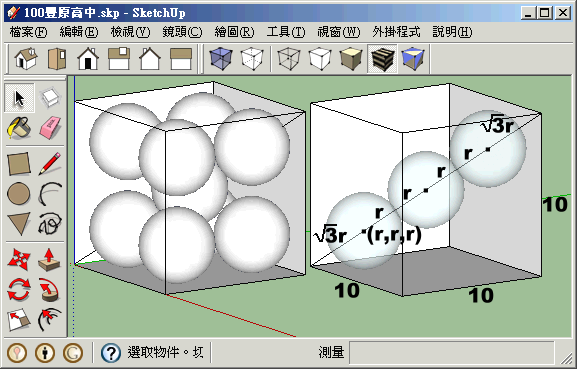
將一個半徑為4公分的水晶球，放入一個邊長為8公分的正方體容器，想在容器的八個角落再塞入八個半徑相同的小水晶球，則小水晶球的最大半徑為多少公分？
[解答]
設小水晶球半徑\(r\)
立方體的斜對角線\(8\sqrt 3  = 4 \cdot 2 + 2r\sqrt 3  + 2r\)
移項即可解出\(r\)
這題考出來算是秒殺題了
關鍵在斜對角線與內接球半徑的關係

110.2.28補充

更多類似問題https://math.pro/db/thread-1268-1-1.html

8.
設\(P\)在拋物線\(y=x^2\)上，且在第一象限內的任意一點，如圖所示，直線\(PB\)與\(x\)軸平行，且交\(y\)軸於\(B\)點；直線\(PA\)是拋物線過\(P\)點的切線，且交\(y\)軸於\(A\)點。若拋物線、直線\(PB\)與\(y\)軸所圍的區域面積為\(R\)，\(\Delta PAB\)的面積為\(T\)，則比值\(\displaystyle \frac{R}{T}=\)？
[解答]
設切點P為\((\sqrt t ,t)\)，可算出切線交y軸於A點\((0, - t)\)
\(\Delta PAB = \frac{1}{2} \cdot 2t \cdot \sqrt t  = t\sqrt t \)
拋物線與y軸、\(\overline {PB} \)所夾面積\(\int_0^{\sqrt t } {(t - {x^2})} dx = \frac{2}{3}t\sqrt t \)
故所求比值為\(\frac{2}{3}\)

10.
已知函數\(f(x)=2x^3+3ax^2+6a(a-1)x+2\)，\((a\in R)\)，若\(f(x)\)的圖形與\(x\)軸相切，且在切點處\(f(x)\)有極小值，則\(a\)值為何？
[解答]
\(f'(x) = 6{x^2} + 6ax + 6(a - 1) = 0\)解得\(x =  - 1,1 - a\)
若\(1 - a >  - 1\)，即\(a < 2\)
\(f(1 - a) = 0\)解得\(a = 2 - \sqrt 3 \)

若\(1 - a <  - 1\)，即\(a > 2\)
\(f(-1) = 0\)，此時\(a\)無解
故答案只有一個