因為有朋友問當中的題目，解完順便放上來。：）

註：感謝 Ellipse 補充～第二題的答案應該為 2366 ，而非 2365.

第一題
試求2011201020092008+1−(2009)22011 的個位數字。
[解答]
令 x=2009，

則 2011201020092008−1=(x+2)(x+1)x(x−1)+1=(x2+x−1)2

所以所求＝(x−1)2011=2008201182011(mod10)

剩下用同餘處理～應該就沒有問題了！：）





第 12 題
如右圖，在ABC中，AB=425，BC=450，CA=510，P為ABC內一點，DEFGHI都過P點，且分別平行ACBCAB，若DE=FG=HI=d，則d=？


解答：

設 BH=xHE=yEC=z，

因為 IHC 與 ABC 相似，所以 BCHC=IHABy+zx+y+z=d425

因為 DBE 與 ABC 相似，所以 BEBC=ACDEx+yx+y+z=d510

因為 GF=GP+PF=BH+EC，所以 x+zx+y+z=d450

將上列三個分式相加，可得 2=1425+1510+1450d 

d=306

第 2 題：
若n是大於(5+2)6 的最小整數，試求n之值？
[解答]
令 p=5+2q=5−2 

則 pq=3 且 p2+q2=14

　 p6+q6=p2+q23−3p2q2p2+q2=2366 

因為 0q1，所以 0q61

　　p6=2366−q6=2365xxx

所以，大於 (5+2)6  的最小整數值為 2366


大於(3+2)6 的最小整數為何？
(建中通訊解題第39期)

[x]表示不大於x的最大整數(高斯符號)，試求[(3+1)8]= ？
(101台南二中，https://math.pro/db/viewthread.php?tid=1335&page=1#pid5262)

113.5.16補充
回答下列與數相關的問題：
(1)若將a=(2+5)20+(2−5)20 展開後，其個位數字為　　　。
(2)若將b=(2+5)20 展開後，其整數部分的末兩位數為　　　。
(113西松高中，https://math.pro/db/viewthread.php?tid=3870&page=1#pid26199)

第 4 題：
設a1a2a10N，試求a1a2a10(a21+1)(a22+1)(a210+1)的最小值。
[解答]
由算幾不等式，可得

　　a21+12a211=2a1 

同理，

　　a22+12a2，a23+12a3，‧‧‧，a210+12a10，

因為上列十個式子的左右兩端都非負，十式連乘可得

　　a21+1a22+1a210+1210a1a2a10 

　　a1a2a10a21+1a22+1a210+11024 

且當等號成立時，a1=a2==a10=1

第 7 題：
將分數n120約分為最簡分數，其中n為小於120的正整數。請問共有多少個不同值的最簡分數，使得它的分子為一位數？
[解答]
120=2335

一、若約到最簡分數後分子為 1，則

　n=2a3b5c，

　其中 a=0123，b=01，c=01

　但 (abc)=(311) 時，n120=1 不是分數，不合，

　有 422−1=15 種可能。

二、若約到最簡分數後分子為 2，則

　n=2a3b5c，

　其中 a=4，b=01，c=01

　　　但是 (abc)=(411) 會讓 n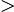120 不合

　有 122−1=3 種可能。

三、若約到最簡分數後分子為 3，則

　n=2a3b5c，

　其中 a=0123，b=2，c=01

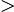　　　但是 (abc)=(321)(221) 會讓 n120 不合

　有 412−2=6 種可能。

四、若約到最簡分數後分子為 4，則

　n=2a3b5c，

　其中 a=5，b=01，c=01

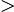　　　但是 (abc)=(511)(501) 會讓 n120 不合

　有 122−2=2 種可能。

五、若約到最簡分數後分子為 5，則

　n=251252253 或 254

　有 4 種可能。

六、若約到最簡分數後分子為 6，則

　n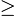2432=144 不可能，此與 n120 相矛盾。

七、若約到最簡分數後分子為 7，則

　n=72a3b5c，

　其中 a=0123，b=01，c=01

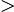　　　但是 (abc)=(311)(211)(111)(301)(310)(201) 會讓 n120 不合

　有 422−6=10 種可能。

八、若約到最簡分數後分子為 8，則

　n=26，有 1 種可能。

九、若約到最簡分數後分子為 9，則

　n=271272274，有 3 種可能。

以上共 15+3+6+2+4+0+10+1+3=44 種。



不知道有沒有碰巧多列或漏列的呢？有勞大家了？

不知道除了條列之外，有沒有更好的做法。感謝。

第 9 題：
在十進位制中，有兩個二位數aa、bb滿足(aa)2+(bb)2=aabb，則aabb=？
[解答]
因為 aa 與 bb 皆有 11 的因數，

所以 aa2 與 bb2 皆有 112 的因數，

亦即 aabb  也有 112 的因數，

而 aabb=1000a+100a+10b+b=11(100a+b)

11(100a+b)1199a+(a+b)11(a+b)

且因為 ab 皆為 0 到 9 的阿拉伯數字，所以 a+b=11

檢查 222+992=10285 不合

　　 332+882=8833aa=88bb=33

　　 442+772=7865 不合

　　 552+662=7381 不合

ps. 考試時候要速度的話，可以先檢查個位數字，

　　如： 222 個位數字為 4，992 個位數字為 1，

　　兩者個位數字和為 5 ，不會是 2 或 9，因此不合，不用真的算出來相加。


　　另解也可以列 122292 的個位數字，

　　然後看有沒有哪兩者相加的個位數字會回到其中一個，

　　然後再條列計算一下，應該也很快。