





原帖由 weiye 於 2013-5-15 09:24 PM 發表
第 10 題:
令 \(P(1+2t,0+t,3-2t)\)
\(\overline{PA}+\overline{PB}\)
\(=\sqrt{\left(2t+2\right)^2+\left(t-2\right)^2+\left(2t+8\right)^2}+\sqrt{\left(2t-22\right)^2+\left(t-2\right)^2+\left(2t-13\right)^2}\)
\(=3\left(\sqrt{\left(t+2\right)^2+2^2}+\sqrt{\left(t-8\right)^2+3^2}\right)\)
...
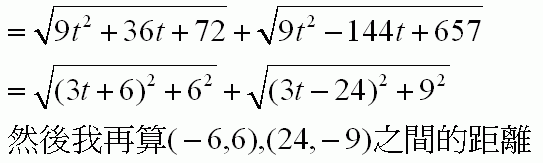


 )
)原帖由 tsusy 於 2013-5-19 08:04 PM 發表
第8題.
\( a_{n}-[a_{n}]=\begin{cases}
\frac{1}{3} & \mbox{, n is odd}\\
\frac{2}{3} & \mbox{, n is even}
\end{cases} \),由此可得 \( a_{n+1}=\begin{cases}
a_{n}+\frac{1}{3} & \mbox{, n is odd}\\
a_{n}+ ...

| 歡迎光臨 Math Pro 數學補給站 (https://math.pro/db/) | 論壇程式使用 Discuz! 6.1.0 |