
標題: 101清水高中 [打印本頁]
作者: Herstein 時間: 2012-6-7 14:14 標題: 101清水高中
如附件,請大家慢慢享用
101.6.10版主補充
以下資料供以後考生參考:
初試最低錄取分數 60分
取15名參加複試,錄取3名
84,72,68,68,65,64,64,64,64,64,62,62,61,60,60
其他,
50~59分 22人
40~49分 42人
30~39分 49人
20~29分 26人
10~19分 32人
0~9分 12人
缺考 13人
共計 211人
[ 本帖最後由 bugmens 於 2012-6-10 09:35 PM 編輯 ]
 附件: 101清水高中.rar (2012-6-7 14:40, 327.19 KB) / 該附件被下載次數 14940
附件: 101清水高中.rar (2012-6-7 14:40, 327.19 KB) / 該附件被下載次數 14940
https://math.pro/db/attachment.php?aid=1205&k=dc8afff359267a884995eb6bd52e7bbc&t=1769635373
作者: tuhunger 時間: 2012-6-8 08:59
第五題
開頭是9: 9 876543210: 後面9碼可選可不選 2^9種 ,例如 後9碼只選中8532 => 98532
開頭是8: 8 76543210: 後面8碼可選可不選 2^8種
....類推 2 10: 後面2碼可選可不選 2^2種
共[2^9+2^8+...+2^2] - [9+8+...+2] - [1+1+...+1]=986(種)
^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^ ^^^^^^^^^^^^^^
三位數以下 只選一個(二位) 都沒選(一位)
作者: natureling 時間: 2012-6-8 11:20 標題: 請教填充2,3,9,11,14,15
感恩...另外,填充第二..為何不能想成圓\(x^2+y^2=1\)和直線\(x+y=5\)最短距離的平方呢?
作者: natureling 時間: 2012-6-8 11:25
提供自己想法,不知對錯...@@
因為要大到小..故0~9只有 10個數,最多為10位數
又要是3位以上,故想成從0~9中選3、4、...10個數字,再按大排到小
故\(C(10,3)+C(10,4)+\ldots+C(10,10)\)
\(=C(10,0)+C(10,1)+\ldots+C(10,10)-C(10,0)-C(10,1)-C(10,2)\)
\(=2^{10}-C(10,0)-C(10,1)-C(10,2)\)
\(=968\)引用:
原帖由 tuhunger 於 2012-6-8 08:59 AM 發表 
第五題
開頭是9: 9 876543210: 後面9碼可選可不選 2^9種 ,例如 後9碼只選中8532 => 98532
開頭是8: 8 76543210: 後面8碼可選可不選 2^8種
....類推 2 10: 後面2碼可選可不選 2^2種
共[2 ...
作者: YungLu 時間: 2012-6-8 12:52
引用:
原帖由 natureling 於 2012-6-8 11:20 AM 發表 
感恩...另外,填充第二..為何不能想成圓 x^2+y^2=1和直線x+y=5 最短距離的平方呢?
1999 | n^2-1909n+2000+1999n
1999 | n^2+90n+2000
1999 | (n+40)(n+50)
故\(n\)最小為\(1949,1959\)
填充13 答案945怎麼來的? 一直都算成525,感謝幫解
作者: dav 時間: 2012-6-8 13:10
引用:
原帖由 natureling 於 2012-6-8 11:20 AM 發表 
感恩...另外,填充第二..為何不能想成圓 x^2+y^2=1和直線x+y=5 最短距離的平方呢?
 可以再試試看
可以再試試看
作者: tuhunger 時間: 2012-6-8 14:55 標題: 回復 3# natureling 的帖子
感恩...另外,填充第二..為何不能想成圓\(x^2+y^2=1\)和直線\(x+y=5\)最短距離的平方呢?
我的方法: 對X微=0 對y微=0. 可得u=某數(忘了), cosv=sinv=1/√2 代進去可解
你的方法: d(O,L)=5√2 /2 , 最短距離平方=[(5√2 -2)/2]^2 =ans 你的也對,應該是你計算錯誤啦
PS:我考試就12分因為加減乘除錯誤,飛走了><
作者: weiye 時間: 2012-6-8 15:15 標題: 回復 3# natureling 的帖子
填充第 2 題~跟 2004 TRML 考題都一樣(數字也沒改)
以前解過,請見 https://math.pro/db/thread-59-1-1.html
作者: JOE 時間: 2012-6-8 16:51 標題: 回復 5# YungLu 的帖子
我跟YungLu有一樣的疑問
填充13 算不出學校公告的答案
另外想請問計算2 感謝
作者: natureling 時間: 2012-6-8 16:52 標題: 感謝各位大大
...@@真的計算錯誤....>"<
作者: shiauy 時間: 2012-6-8 17:35
17題我算的答案是2/9,不知3/10怎麼求出的
計算第二
http://zh.wikipedia.org/wiki/%E7%A7%91%E8%B5%AB%E9%9B%AA%E8%8A%B1
我是找第n個圖與第n-1圖的面積關係
\[{T_n} = {T_{n - 1}} + \frac{{\sqrt 3 }}{4}{(\frac{1}{{{3^{n - 1}}}})^2}3 \cdot {4^{n - 2}}\]
\[{T_n} = {T_{n - 1}} + \frac{{3\sqrt 3 }}{{16}}{(\frac{4}{9})^{n - 1}}\]
\[{T_n} = \frac{{\sqrt 3 }}{4} + \frac{{3\sqrt 3 }}{{16}}(\frac{{\frac{4}{9}(1 - {{(\frac{4}{9})}^{n - 2}})}}{{1 - \frac{4}{9}}}) = \frac{{\sqrt 3 }}{4} + \frac{{3\sqrt 3 }}{{20}}(1 - {(\frac{4}{9})^{n - 2}})\]
\[{T_n} \to \frac{{\sqrt 3 }}{4} + \frac{{3\sqrt 3 }}{{20}} = \frac{{2\sqrt 3 }}{5}\]
[ 本帖最後由 shiauy 於 2012-6-8 06:03 PM 編輯 ]
作者: YungLu 時間: 2012-6-8 18:20 標題: 回復 11# shiauy 的帖子
蔡宗龍老師有篇專題文章在講"碎形"
文中 P.4 ~ P.5 有提到本題的面積及周長的解法
大家可以參考看看
http://ppt.cc/MsXE
作者: tacokao 時間: 2012-6-8 18:42 標題: 回復 11# shiauy 的帖子
第17題的甲袋轉移矩陣A為 2R 1R1W 2W
2R [ 1/3 1/3 0 ] [ a ]
1R1W[ 2/3 1/2 1 ] X= [ b ]
2W [ 0 1/6 0 ] [ c ]
甲袋為2R的機率為a,1R1W機率為b,2W機率為c,a+b+c=1,就長期而言,AX=X,a=1/2b,c=1/6b,則b=3/5
a=3/10,c=1/10。所以P(2R)=a=3/10。
[ 本帖最後由 tacokao 於 2012-6-8 06:49 PM 編輯 ]
作者: arend 時間: 2012-6-8 19:13
請教填充第4題
沒有頭緒
這題好像在某教甄看過
就是想不出來
謝謝
作者: shiauy 時間: 2012-6-8 19:27
引用:
原帖由 arend 於 2012-6-8 07:13 PM 發表 
請教填充第4題
沒有頭緒
這題好像在某教甄看過
就是想不出來
謝謝
所以不管轉換幾次,\(A+B=-16+25=9\)
作者: agan325 時間: 2012-6-8 22:02 標題: 回復 13# tacokao 的帖子
多謝你的細心解說!
害我寫出來矩陣\(A\)....結果就直接寫\(\displaystyle \frac{1}{6}\)....= =
作者: tacokao 時間: 2012-6-8 22:46
想請教填充第9及16題,感謝大家!!!
作者: shiauy 時間: 2012-6-8 23:38
引用:
原帖由 tacokao 於 2012-6-8 10:46 PM 發表 
想請教填充第9及16題,感謝大家!!!
可以參考老王畫的圖
http://tw.myblog.yahoo.com/jw!ozHXUsWHHh7UxM0Y2TXK_uEdXwGqCw--/photo?pid=4836
\[\sqrt {25 - {d^2}} + \sqrt {13 - {d^2}} = 2\sqrt {18 - {d^2}} \]
平方後移項在平方可得d=3
#16
\[{x^3} - 2{x^2} + 2x - 1 = (x - 1)({x^2} - x + 1)\]
\[f(x) = (x - 1){Q_1}(x) - 5\]
\[=(x + 1)({x^2} - x + 1){Q_2}(x) - {x^2} - 3x - 1\]
\[=({x^2} - x + 1){Q_3}(x) - 4x\]
令\[f(x) = (x - 1)({x^2} - x + 1)Q(x) + a({x^2} - x + 1) - 4x\]
\[f(1) = - 5 = a - 4\]
\[a = - 1,R(x) = - {x^2} - 3x - 1\]
湊合著看,從mathtype貼過來都變置中了…
[ 本帖最後由 shiauy 於 2012-6-8 11:41 PM 編輯 ]
作者: WAYNE10000 時間: 2012-6-9 10:12 標題: 請教填充10 12 13 20
12.
我一直算\(-2\)到2之間
20.
\(a\)不是大於0就好
感謝賜教 謝謝
作者: tacokao 時間: 2012-6-9 11:15 標題: 回復 19# WAYNE10000 的帖子
填充第20題,一次微分之後會得到極值-1,0,2,因為與\(x\)軸有三個交點,就分兩個case看
(1)\(f(-1)*f(0)<0\)及\(f(0)*f(2)>0\),這個case的\(a\)範圍無交集
(2)\(f(-1)*f(0)>0\)及\(f(0)*f(2)<0\)就可以得到\(5<a<32\)囉!!!
作者: tacokao 時間: 2012-6-9 11:15 標題: 回復 18# shiauy 的帖子
感謝一心老師,我看懂了!!!謝謝您的解說!!!!
作者: agan325 時間: 2012-6-9 13:06 標題: 回復 11# shiauy 的帖子
多謝一心老師
看到這題讓我想到桃園縣高中聯招的計算題
但是這次還是一個小環節出問題...
下次計算要更小心
作者: pizza 時間: 2012-6-9 15:55
能否請問填充10,11,13,19,謝謝
作者: shiauy 時間: 2012-6-9 16:45
引用:
原帖由 pizza 於 2012-6-9 03:55 PM 發表 
能否請問填充10,11,13,19,謝謝
已知\(\Delta ABC\)之內切圓切\(\overline{BC}\)於\(D\),若\(\overline{AB}=4\),\(\overline{BC}=6\),\(\overline{CA}=5\),則\(\overline{AD}\)長為 。
http://www.ptt.cc/bbs/SENIORHIGH/M.1316942234.A.5D9.html
#11
99台中一中 第8題
https://math.pro/db/viewthread.php?tid=929&page=1#pid1991
#13
101中正預校第14題
https://math.pro/db/viewthread.php?tid=1383&page=2#pid6119
#19
\[{a_n} = {a_{n - 1}} + 2\frac{{(2 + 2(n - 1))}}{2} - 1 = {a_{n - 1}} + 2{n^2} - 1\]
這份試卷很多考古題,太多題不會就表示你考古題作的還不夠
作者: 阿光 時間: 2012-6-9 19:56
想請教填充第6題,謝謝
作者: YungLu 時間: 2012-6-9 20:30 標題: 回復 24# shiauy 的帖子
#13
101中正預校第14題
https://math.pro/db/viewthread.php?tid=1383&page=2#pid6119
我的方法也是這個辦法,\(12600=2^3*3^2*5^2*2\)
算出來是525,公布的答案卻是945
作者: tuhunger 時間: 2012-6-9 20:34
引用:
原帖由 阿光 於 2012-6-9 07:56 PM 發表 
想請教填充第6題,謝謝
PS: 有誰可以教我 怎直接用MathType打數學符號在上面
 圖片附件: 未命名.jpg (2012-6-9 20:34, 10.72 KB) / 該附件被下載次數 7879
圖片附件: 未命名.jpg (2012-6-9 20:34, 10.72 KB) / 該附件被下載次數 7879
https://math.pro/db/attachment.php?aid=1216&k=8e800444163d75aef6143a0027eae7c3&t=1769635373

作者: shiauy 時間: 2012-6-9 20:59
答案給錯了啊
945是用126000算出來的
作者: Jacob 時間: 2012-6-10 13:22 標題: 想請問第三題與第15題
想請問第三題與第15題 剩這兩題不會算 謝謝
還有就是怎樣才可以把算法打上來 Math pro 的語法如何打呢?
謝謝
作者: tacokao 時間: 2012-6-10 14:04 標題: 回復 29# Jacob 的帖子
第3、15題,鋼琴大已解。
http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&t=2836
作者: matric0830 時間: 2012-6-11 09:25 標題: 請問第18題
請問第18題
作者: weiye 時間: 2012-6-11 09:47 標題: 回復 31# matric0830 的帖子
第 18 題:
\(\displaystyle P(X\geq Y)=\frac{C^{N+1}_2+C^{N+1}_1\cdot1}{C^{N+1}_1\cdot C^{N+1}_1}=\frac{N+2}{2\left(N+1\right)}\)
作者: matric0830 時間: 2012-6-11 10:20 標題: 回復 32# weiye 的帖子
老師謝謝!我知道我的問題出在哪了:)
作者: dav 時間: 2012-6-11 12:48
清水高中的第一題很有趣
是國一課本習作的題目耶O_O... 哈
作者: dennisal2000 時間: 2012-6-14 16:57 標題: 回復 18# shiauy 的帖子
想請教第16題 以\(x^2 -2x^2+2x-1\)除\(f(x)\)的餘式\(-4x\)是怎麼得到的?
作者: peter579 時間: 2012-6-16 00:57
[quote]原帖由 dennisal2000 於 2012-6-14 04:57 PM 發表 
\(x^2 -2x^2 + 2x -1 =(x-1)( x^2 -x+1)\)
\((x^2 -x+1)(x+1)=x^3+1\)
令\(x^3=-1\)代入即可得到答案。
作者: blue329456 時間: 2012-6-18 22:38 標題: 填充第17題
長期之後
樣本空間為 5顆球取2顆球---------> \(C(5,2)=10\)
事件為 三紅球之中取二顆紅球----> \(C(3,2)=3\)
所以機率為\(\displaystyle \frac{3}{10}\)
作者: youngchi 時間: 2012-6-27 15:31
引用:
原帖由 shiauy 於 2012-6-8 07:27 PM 發表 
(a-b+c)+(2b-a)=b+c
所以不管轉換幾次,A+B=-16+25=9
但大家都是用相同觀念解答,我想請問
究竟可否用矩陣求解?
作者: katama5667 時間: 2012-7-2 14:06
引用:
原帖由 WAYNE10000 於 2012-6-9 10:12 AM 發表 
12 我一直算 -2到2之間
則\(|z_{1}|^2\geq |z_{2}|^2\)
\(\Rightarrow x^4+(x^2+4)\geq (x^2+t)^2\)
\(\Rightarrow (2t-1)x^2+(t^2-4)\leq 0\) 恆成立
則
(1)若 \(2t-1=0\),\(\Rightarrow t^2-4\leq 0\),所以 \(t=\frac{1}{2}\) 合
(2)若 \(2t-1\neq 0\),則
\(2t-1<0\) 且 \(-4(2t-1)(t^2-4)\leq 0\)
\(\Rightarrow t<\frac{1}{2}\) 且 \((2t-1)(t+2)(t-2)\geq 0\)
\(\Rightarrow t<\frac{1}{2}\) 且 \((2t-1)(t+2)(t-2)\geq 0\)
\(-2\leq t <\frac{1}{2}\)
故得 \(-2\leq t \leq \frac{1}{2}\)
[ 本帖最後由 katama5667 於 2012-7-3 10:48 PM 編輯 ]
作者: larson 時間: 2012-7-3 16:43
或解的範圍要改為−2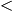 t
t 1/2希望出題老師或教授們要多審題,否則我們在考場可能會以為自己算錯了!
1/2希望出題老師或教授們要多審題,否則我們在考場可能會以為自己算錯了!
作者: 阿光 時間: 2012-8-7 21:35
想請教填充第6題的詳解,謝謝
作者: tsusy 時間: 2012-8-7 21:58 標題: 回復 41# 阿光 的帖子
填充 6. 注意積分的區域的正負
\( \int x^{2}-ax+adx=\frac{x^{3}}{3}-\frac{ax^{2}}{2}+ax+c \)
\( 0=\alpha-\beta=\int_{0}^{q}ydx=\frac{q^{3}}{3}-\frac{aq^{2}}{2}+aq\Rightarrow2q^{2}-3aq+6a=0 \)
又 \( q^{2}-aq+a=0\Rightarrow-aq-4a=0\Rightarrow q=4 \) , \( a=\frac{16}{3} \) 。
作者: panda.xiong 時間: 2013-5-1 20:41
有計算第一題的答案嗎??
作者: thepiano 時間: 2013-5-1 21:20
計算題第 1 題答案
(1)
x > 1
x - y - 5 < 0
2x + y - 7 < 0
y < -1
0 < x < 1
x - y - 5 < 0
2x + y - 7 < 0
y > -1
(2) 略
(3) 15
作者: panda.xiong 時間: 2013-5-1 22:52 標題: 回復 44# thepiano 的帖子
謝謝老師。
請問填充第18題,前面有老師解過,但怎麼解釋呢?
作者: thepiano 時間: 2013-5-2 08:12
第 18 題
\(X\)和\(Y\)分別是\(0~n\)這\((n+1)\)個數中的其中之一
求\(X \ge Y\)的機率
weiye 老師的解法中的分子
\(C(n,2)\)是\(X>Y\)的情形數
\(C(n,1)*1\)是\(X=Y\)的情形數
作者: cefepime 時間: 2016-9-25 23:47
填充題 15.
先考慮 OA 射線上,點 D' 的位置: 在此 F 是 D' 與 C 的中點。
A (1, 3),F (1, 1),D' (s, 3s),C (t, 0)
⇒ D' (2/3, 2),C (4/3, 0)
因 D' 落在 OA 線段上,故 a△OCD' 即為所求 = (1/2)*(4/3)*2 = 4/3
| 歡迎光臨 Math Pro 數學補給站 (https://math.pro/db/) |
論壇程式使用 Discuz! 6.1.0 |

 可以再試試看
可以再試試看 

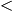 t
t 1/2希望出題老師或教授們要多審題,否則我們在考場可能會以為自己算錯了!
1/2希望出題老師或教授們要多審題,否則我們在考場可能會以為自己算錯了!