計算第 6 題
設\(f(1)=-1\)，\(\displaystyle f(2)=-\frac{1}{2}\)，對所有大於等於3的整數\(n\)，\(f(n)\)滿足：\(n\cdot f(n)=(n-1)\cdot f(n-1)+f(n-2)\)。試求\(f(n)\)。
[解答]
n[f(n) - f(n - 1)] = - [f(n - 1) - f(n - 2)]
g(n) = f(n) - f(n - 1)
g(n)/g(n - 1) = -1/n
[g(3)/g(2)][g(4)/g(3)]……[g(n)/g(n - 1)] = (-1)^n * [1/(n!/2)] = (-1)^n * (2/n!)
g(2) = f(2) - f(1) = 1/2
g(n) = (-1)^n * (1/n!)

g(3) = f(3) - f(2) = -1/3!
g(4) = f(4) - f(3) = 1/4!
:
:
g(n) = f(n) - f(n - 1) = (-1)^n * (1/n!)
f(n) = -1/2 - 1/3! + 1/4! - …… + (-1)^n * (1/n!)

更正計算題第7題
有一款手機遊戲《花女策珂戰》，遊戲中有抽卡機制，可以透過抽卡來抽得角色。每次抽卡都會抽出一張角色卡，抽卡有可能會抽到重複的角色卡。而角色卡有等級之分，最好的等級是SSR，其餘等級都稱為廢卡。此遊戲抽卡時會有保底機制，其機制為：若連續抽卡99次，皆抽到廢卡，則下一次抽卡必定抽得SSR，而必定抽到SSR的這次抽卡稱為觸發保底。此機制會永久有效，即只要抽到SSR卡，不論是直接抽到或者觸發保底抽到，只要再次發生連續抽卡99 次皆抽到廢卡，則下一抽也必定是抽到SSR。設尚未觸發保底時，每次抽卡抽到 SSR的機率皆為定值p，且\(0<p<1\)。若抽卡250次，試求抽到SSR的次數期望值（試以\(p\)表示答案）。
[解答]
設第\(k\)次抽到SSR的機率為\(p_k\)
\(p_1=p_2=...=p_{99}=p\)
\(p_{100}=p+(1-p)^{99}(1-p)=p+(1-p)^{100}\)
\(p_{101}=p+p_1(1-p)^{99}(1-p)=p+p_1(1-p)^{100}\)
\(p_{102}=p+p_2(1-p)^{99}(1-p)=p+p_2(1-p)^{100}\)
...
\(p_{250}=p+p_{150}(1-p)^{99}(1-p)=p+p_{150}(1-p)^{100}\)
因此250次可抽得SSR張數的期望值為
\(p_1+p_2+...+p_{250}\)
\(=250p+[1+p_1+p_2+...+p_{150}](1-p)^{100}\)
\(=250p+[1+p_1+p_2+...+p_{99}](1-p)^{100}+[p_{100}+p_{101}+...+p_{150}](1-p)^{100}\)
\(=250p+[1+99p](1-p)^{100}+[51p+(1+50p)p^{100}](1-p)^{100}\)
\(=250p+(1+150p)(1-p)^{100}+(1+50p)(1-p)^{200}\)

太太太感謝 swallow7103老師、鋼琴老師、Jimmy92888老師了！！！！！

引用:

原帖由 Jimmy92888 於 2024-6-18 07:49 發表
更正計算題第7題

設第\(k\)次抽到SSR的機率為\(p_k\)
\(p_1=p_2=...=p_{99}=p\)
\(p_{100}=p+(1-p)^{99}(1-p)=p+(1-p)^{100}\)
\(p_{101}=p+p_1(1-p)^{99}(1-p)=p+p_1(1-p)^{100}\)
\(p_{102}=p+p_2(1-p)^{99}(1-p) ...

漂亮的作法，我也提供一個想法

如果沒有保底機制，則期望值為：\(250p\)

有了保底機制後，就需要補上連續99抽都不是好卡時，第100抽仍不是好卡時，保底機制所提供的一張。

若保底機制是發生在第1~100抽，則提供：\((1-p)^{99}*(1-p)=(1-p)^{100}\)

因為保底機制需要連續抽到爛卡，所以除了第1~100抽之外，其他觸發保底的情況都是先抽到一張SSR，再來連續99抽與不是好卡
故保底機制的完整過程是在第2~101抽、第3~102抽、第4~103抽、......、第151~250抽所發生、所提供的SSR期望值為：\(p*(1-p)^{100}×150=150p(1-p)^{100}\)


除了第1~100抽觸發保底之外，其他是先抽到一張SSR，再來連續99抽，就會觸發保底機制。但這個「先抽到SSR」的來源，可能是本來運氣好就抽到的，也有可能來自觸發保底所抽到的SSR
故上述還需要補上保底機制觸發後又再次觸發保底的狀況：
第1抽~100抽&第101抽~第200抽：\((1-p)^{100}×(1-p)^100=(1-p)^{200}\)
第2抽~101抽&第102抽~第201抽、第3抽~102抽&第103抽~第202抽、......、第51抽~150抽&第151抽~第250抽：\(p*(1-p)^{100}×(1-p)^{100}×50=50p(1-p)^{200}\)

故所求為：
\(250p+(1-p)^{100}+150p(1-p)^{100}+(1-p)^{200}+50p(1-p)^{200}=250p+(1-p)^{100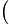}\left(1+150p+(1-p)^{100}+50p(1-p)^{100}\right)\)

請教 第二部份第3題，謝謝

計算第 3 題
試找出所有函數\(f\)：\(R\to R\)，滿足\(\forall x,y\in R\)，\(f(x-y)=f(x)+f(y)-2xy\)。
[解答]
x = y = 0 代入，可得 f(0) = 0
x = y = k (k 是實數) 代入，可得 f(k) = k^2
f(x) = x^2

謝謝大大~~~

引用:

原帖由 thepiano 於 2024-8-15 22:41 發表
計算第 3 題
x = y = 0 代入，可得 f(0) = 0
x = y = k (k 是實數) 代入，可得 f(k) = k^2
f(x) = x^2