已知abc皆為正數，且以b+c、abc 、b2+7bc+c2 為長度的線段恆能構成三角形，則a的範圍為　　　。
請教各位老師，非常感謝

113.3.31補充
所問題目出自111高中數學能力競賽，故將文章標題改為"111高中數學能力競賽"
官方網頁https://sites.google.com/mail.nk ... /%E9%A6%96%E9%A0%81
題目以決賽總報告公布
https://drive.google.com/file/d/ ... view?usp=share_link

\begin{align}   & \sqrt{{{b}^{2}}+7bc+{{c}^{2}}}-(b+c)<\sqrt{abc}<\sqrt{{{b}^{2}}+7bc+{{c}^{2}}}+(b+c) \\ & \sqrt{\frac{b}{c}+7+\frac{c}{b}}-\sqrt{\frac{b}{c}+2+\frac{c}{b}}<\sqrt{a}<\sqrt{\frac{b}{c}+7+\frac{c}{b}}+\sqrt{\frac{b}{c}+2+\frac{c}{b}} \\ & \frac{5}{\sqrt{\frac{b}{c}+7+\frac{c}{b}}+\sqrt{\frac{b}{c}+2+\frac{c}{b}}}<\sqrt{a}<\sqrt{\frac{b}{c}+7+\frac{c}{b}}+\sqrt{\frac{b}{c}+2+\frac{c}{b}} \\ & 1=\frac{5}{\sqrt{2+7}+\sqrt{2+2}}<\sqrt{a}<\sqrt{2+7}+\sqrt{2+2}=5 \\ & 1<a<25 \\ \end{align}

感謝老師

求所有整數x,y,z滿足\cases{x+y+z=4\cr x^3+y^3+z^3=88}
彰雲嘉區複賽試題一

設x,y,z均為整數且滿足\cases{x^3+y^3+z^3=132\cr x+y+z=6}，求|\;x|\;+2|\;y|\;+|\;z|\;的所有可能值為何？
(105師大附中代理，https://math.pro/db/thread-2543-1-1.html)

若正實數a,b滿足log_9 a=log_{12}b=log_{16}(a+b)，則\displaystyle \frac{b}{a}=　　　。
第一區(花蓮高中)筆試二試題

若0\le x \le 2\pi，則滿足tan^2 x-9tanx+1=0的所有x值之和為　　　。
第一區(花蓮高中)筆試二試題
(1989AHSME，https://math.pro/db/viewthread.php?tid=1880&page=1#pid10245)

已知實數x滿足拉馬努金等式\displaystyle \root 3 \of{\root 3\of 2-1}=\frac{1-\root 3\of 2+\root 3 \of 4}{x}，求實數x的值。(須以最簡單形式表示)
第一區(花蓮高中)口試試題
https://math.pro/db/viewthread.php?tid=1041&page=1#pid2840

113.1.27補充
設四邊形有一外接圓且有一內切圓，其四邊邊長分別為42,54,78,66。若最長邊被內切圓的切點分成長度為x,y兩線段，則數對(x,y)=　　　。
第一區(花蓮高中)筆試二試題

四邊形面積之旅
陳敏晧(國立蘭陽女中)
本文從數學學科能力競賽試題出發，研究最著名的四邊形面積公式－布雷特施奈德公式，比較其與婆羅摩笈多公式的差異，討論柯尼茲公式及道格拉斯．米契爾的文章，引入三角函數討論給定兩對角線長度及夾角的四邊形面積及給定兩對邊中點連線長度及其夾角的四邊形面積，再從三角形面積延伸到四邊形面積，推廣鞋帶公式及皮克公式，文中省略特定形狀的四邊形(如正方形、長方形、平行四邊形、梯形等)。四邊形面積公式雖然不若三角形面積公式的多元呈現，但是，數學成份的融入卻是毫不遜色，絕對值得用心研究。
數學學科中心第191期電子報，https://ghresource.k12ea.gov.tw/ ... a2c69182112d75b514b

已知函數序列f_1(x)=\sqrt{x}、f_2(x)=\sqrt{x+\sqrt{x}}、f_3(x)=\sqrt{x+\sqrt{x+\sqrt{x}}}、\ldots，依此類推。試求方程式f_{10}(x)=2022的所有實數解(四捨五入取到整數)。

謝謝

偷懶我就不寫證明，寫一些想法供參考

1. 推(猜)測 f_{10} (x) ，的 10 是一個不重要的數，換成 100 , 999 亦無妨

2. 也就是改成 f_{999} (x) =2022 的答案及作法，應該也沒什麼變化

3. 故猜測固定正實數 x 時， < f_n(x)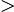> 應該是一個「看起來」很快收斂的數列

4. 例：若 x=100 , f_1(x) = 10 , f_2(x) \approx 10.488 , f_3(x) \approx 10.511 , f_4(x) \approx 10.512 ...

也可以再試其他數字例如若 x=10000 ，不難發現，只有 f_1(x) 到 f_2(x) 增加約 0.5 ，之後數列以極微小的幅度再增加

5. 延續上可的猜測，可推(猜)得 f_1(x) = \sqrt{x} \approx 2022 -0.5 \Rightarrow x \approx 2022^2 -2022 +0.25

6. 上面的估計可能是對的，但有點討厭，在平方(去根號) 時，會讓誤差放大，降低對答案是 2022^2 -2022 的信心

所以寫證明的時候，想用 5. 的估計的話，應該不太容易。回到原方程式，整理可得以下：

f_{10}(x) = 2022 \Rightarrow x + f_9(x) =2022^2 \Rightarrow x = 2022^2 - f_9(x) \approx 2022^2 -2022

剩下的就是認真估計 f_9(x)

請問一下各位大神,111學科能力競賽是否還沒有各複賽的解答,謝謝