計算一的Mt
要考慮到會繞著行星轉吧

計算1
已知一平面上，行星E以圓形軌道逆時針繞行恆星S，行星E的衛星M以圓形軌道逆時針繞行行星E。阿宗觀察行星E繞行恆星S一圈需時500天，衛星M繞行行星E一圈需時50天，試回答下列問題：
(1)若阿宗將恆心S的位置定為坐標原點(00)，對於阿宗而言第0天時行星E的坐標在(4000)，衛星M的坐標在(4010)。求第t天時，衛星M的坐標。
(2)承上題，若SEM 在第0天時第一次等於180，求下一次SEM=180 時是第幾天。
[解答]

選擇2
已知方程式2xsin(x)=1，且x[03]，則此方程式有幾個解？
(A)1　(B)2　(C)3　(D)4
[解答]
答案如附件

已知橢圓的一頂點為(03)，F1(−40)、F2(40)為其焦點，若點A(11)，P為上的動點，則PA+PF2的最大值為　　　。
[解答]
設R為直線F1A在第三象限與橢圓的交點，
則PF2+PAPF2+PF1+AF1=RF2+RF1+AF1，
所以當P=R時有最大值10+AF1=10+26 

註：若改成第一象限的交點，就變最小值。

設n為正整數，定義n的各位數的數字和為f(n)，例如：f(2023)=2+0+2+3=7，f(135)=1+3+5=9，則滿足f(n)+n=2023的所有正整數n的和為　　　。
[解答]
因為f(n)+n=2023，所以n2023，
此範圍內f(n)最大是n=1999時，所以f(n)f(1999)=28，
於是n1995，接下來只要測試n=1995到2022這個範圍的數即可。

2000到2009與2020到2022為偶數，不可能。
1995到1999這段遞增，可知1997是一解。
2010到2019這段遞增，可知2015是一解。

所以所有解為1997+2015=4012

X為有限集合，定義函數f(X)為X內最大的數，減第二大的數，加第三大的數，減第四大的數，，依此類推。
例如：f(36101)=10−6+3−1=6，f(361024)=10−6+4−3+2=7。
若A=1234112，而X為A中的非空子集，則所有f(x)的和為　　　。
[解答]
所有不包含112的集合X，其f(X)+f(X∪112)=112。
所以只要計算112出現幾次即可，因此總和為112×2111。

已知方程式2xsin(x)=1，且x[03]，則此方程式有幾個解？
(A)1　(B)2　(C)3　(D)4
[解答]
亦即求兩圖形y=x1與y=2sin(x)的交點數。
易知在x(23)時有兩解，與x=21時有一解。
又因為x=21時y=x1凹向上，y=2sin(x)凹向下，所以x(211)還會有一解。
共四個解。

註：13樓有畫y=sin(x)與y=12x示意圖。

一疊撲克牌共10張，某種洗牌方式如下：洗完一次後，原第6張會變第1張，原第1張變第2張，原第7張變第3張，原第2張變第4張，…依此類推；換句話說，就是原來的第1到10張，會依序移到第24681013579張。若用此種洗牌方式連續洗了2023次後，則第10張牌會是一開始的第幾張牌？
(A)第1張　(B)第4張　(C)第6張　(D)第9張
[解答]
每次的洗牌，就是一個排列的函數，依題意
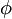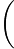=122436485A61738597A9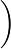=(12485A9736) 
此為10-cycle，所以10次一循環。
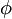2023(x)=10=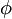3(x)所以x=4(就A往前數3個)

我覺得這題很不錯，基本的代數群論，改成易懂的情境。

引用:

原帖由 Ellipse 於 2023-4-15 23:28 發表
像這種不公布 非選擇題答案
考生不知道是否有被改錯
實在是不負責任的做法

不知為什麼主辦不公布答案，
據我所知，出題教授都會給答案。

引用:

原帖由 Ellipse 於 2023-4-15 23:28 發表

像這種不公布 非選擇題答案
考生不知道是否有被改錯
實在是不負責任的做法

去年臺北市聯招還有公布填充題答案和計算題簡答，今年直接省略
報名費收那麼多，結果數學科有的題目國中生就會做，有些抄得很高興
跟全國聯招比起來，還有很大的進步空間
那些市立前幾志願高中被加入聯招應該很不願意