107.5.30試題疑義公告
填充第6題
1.填充第6題所指的區域
R是由「拋物線
y=x2、直線
x=0及直線
y=1所圍成的區域」;這個區域
R有兩種可能(一個位於第一象限、另一個位於第二象限);但不管哪一種可能,區域
R繞著直線
y=2旋轉所得的旋轉體之體積皆為
1528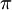
。
2.應考者提供的解法是將以上的兩個可能區域合併計算,得答案為
1528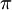
 2=1556
2=1556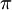
。然而,此種解法所對應的題目敘述應該是「…
R代表由拋物線
y=x2及直線
y=1所圍成的區域…」。
3.出題者的用意是希望應考者能將兩種可能的
R擇一來計算即可(因為兩種算出來的結果相同),但卻因此造成一個模糊空間,使得應考者分別將兩種可能區域
R的旋轉體之體積(
1528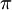
)算出,再合併為
1556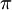
。
4.基於此應考者已能先正確算出
1528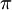
,所以其(合併兩區域所得的)答案
1556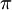
也給分。