15.
在
 ABC
ABC中,
AB=6 BC=4
BC=4 CA=5
CA=5,圓
O1 O2
O2 O3
O3為
 ABC
ABC的三個旁切圓,圓
O1和
BC相切於
D,圓
O2和
CA相切於
E,圓
O3和
AB相切於
F。試求
 ABC面積
ABC面積 DEF面積=
DEF面積= ?
[解答]
r3(tan(A/2)+(tan(B/2))=c
AEF=1/2*(r3tan(A/2))(r2tan(A/2))*sinA
=1/2*c/(1+tan(B/2)/tan(A/2))*b/(1+tan(C/2)/tan(A/2))*sinA
ABC=1/2*bc*sinA , tan(A/2)=
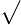 (s−b)(s−c)
(s−b)(s−c) (s(s−a))
(s(s−a))
AEF/ABC=1/{[1+(s-a)/s-b)][1+(s-a)/(s-c)]}=(s-b)(s-c)/(cb)=a(s-b)(s-c)/(abc)
或者 AF=r3*tan(A/2)=ABC/(s-c)*
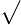 (s−b)(s−c)
(s−b)(s−c) (s(s−a))
(s(s−a))
=
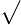 s(s−a)(s−b)(s−c)
s(s−a)(s−b)(s−c) /(s-c)*
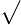 (s−b)(s−c)
(s−b)(s−c) (s(s−a))
(s(s−a)) =s-b
同理AE=s-c
AEF/ABC=(s-b)(s-c)/(cb)=a(s-b)(s-c)/(abc)
a=4,b=5,c=6,s-a=7/2,s-b=5/2,s-c=3/2
所求=1-(4*5/2*3/2+5*7/2*3/2+6*7/2*5/2)/(4*5*6)=7/32
13.
設
x1 x2
x2 x3
x3為方程式
 2014x3−4029x2+2=0
2014x3−4029x2+2=0 的三個實數根,試求
x2(x1+x3)之值
。
[解答]
f(-1)<0,f(0)>0,f(1)<0,f(1000000)>0 =>-1<x1<0<x2<1<x3
令t=
 2014
2014 ,
則 tx^3-(2t^2+1)x^2+2=0 => (-2x^2)t^2+(x^3)t+(-x^2+2)=0
=> ((x)t-1)((-2x)t+(x^2-2))=0 => x=1/t=x2 or x^2-2xt-2=0 =>x1x3=-2
x1x2+x1x3+x2x3=0 => 所求=-x1x3=2