麻煩大家明天要提試題申訴小弟實力不夠大約找到二題答案錯的感謝大家
七題21 24 25 26 28 29 30
21.
已知
 =9t
=9t且
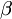 =12t
=12t,其中
t為一數,若
 +
+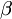 =16t
=16t,則

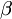
 2+
2+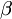 2=
2=?
(A)1 (B)
2 5
5 (C)
 5
5 (D)
2 5
5
24.
如圖,正方形
ABCD之面積為64平方公分,正方形
CEFG之面積為36平方公分,
DE與
BF交於
P點,若
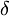 BDP
BDP之面積為
a+cb平方公分(帶分數),其中
a b
b c
c為正整數,
c b
b,且
b c
c互質,則
a+b+c之值為多少?
(A)68 (B)69 (C)70 (D)71


25.
設
a b
b c
c均為正數,且滿足
a2+b2−c2=0的關係;試問:
ca+b的最小值為多少?
(A)
3 3
3 (B)
2 2
2 (C)
21 (D)
 2
2
26.
已知有13個相異的數
a1 a2
a2 a3
a3



 a13
a13,其中至少有3個正數,且正好有
n個負數。今將這13個數中任意二個數相乘,共有91個乘積;如果其中正好有22個數是負數,則
n=?
(A)2 (B)3 (C)10 (D)11
28.
如圖所示,以
O點為圓心,
\overline{AB} 為圓
O 的直徑,弦
\overline{CD} 垂直
\overline{AB} 且與
\overline{AB} 交於
E 點;如果
\overline{AB} 的長度為二位整數,而
\overline{CD} 的長度正好是此二位數的個位數字與十位數字互換位置;若已知
\overline{OE} 的長度為正分數,則
\overline{AB} 的長度為多少?
(A)65 (B)74 (C)83 (D)92


29.
如圖,正方形
ABCD 中,其邊長為1,將每邊作
n 等分,其中
n 為正整數,且點
E,F,G,H 都是各邊上的等分點,使得
\displaystyle \overline{BE}=\overline{CF}=\overline{DG}=\overline{AH}=\frac{1}{n} ;分別作
\overline{AF},\overline{CH},\overline{BG},\overline{DE} ,此四線段分別交於
P,Q,R,S 四點。如果四邊形
PQRS 的面積為
\displaystyle \frac{1}{421} ,試問
n 值為多少?
(A)14 (B)15 (C)16 (D)17


30.
在矩形
ABCD 的較長邊
\overline{AB} 上取一點
Q ,又在較短邊
\overline{AD} 上取一點
P ,使得
\delta PAQ ,
\delta QBC 和
\delta CDP 的面積皆相等,
\displaystyle \frac{\overline{AQ}}{\overline{QB}}= ?
(A)
\displaystyle \frac{1+\sqrt{2}}{2} (B)
\displaystyle \frac{1+\sqrt{3}}{2} (C)
\displaystyle \frac{\sqrt{5}-1}{2} (D)
\frac{1+\sqrt{5}}{2}
[
本帖最後由 bugmens 於 2014-11-11 07:38 AM 編輯 ]