as title
Let's enjoy it!

4.
有　　組實數數對(ab)，使得(a+bi)2002=a−bi
(A)1001　(B)1002　(C)2001　(D)2002　(E)2004
(2002AMC12，http://www.artofproblemsolving.com/Forum/viewtopic.php?p=899529)


5.
將一矩形(邊長均為整數)的角減去一個三角形後形成一個新的五邊形，今知此五邊形之邊長為13,19,20,25,31(不一定照順序成五邊形)，則此五邊形之面積為多少？
(A)600　(B)625　(C)680　(D)720　(E)745
(1995AHSME，http://www.artofproblemsolving.com/Forum/viewtopic.php?p=373524)


6.
一數列依照下列的順序，1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,…以1分隔成多個區塊，而第n個區塊中有n個2，則試問到第1234項之總和為多少？
(A)1997　(B)2419　(C)2431　(D)2447　(E)2511
(1996AHSME，http://www.artofproblemsolving.com/Forum/viewtopic.php?p=418639)


8.
由(0,0)、(2,0)、(2,1)、(0,1)四點所圍成的四邊形中任選一點P，則P到原點的距離小於P到(3,1)的距離之機率為何？
(A)21　(B)32　(C)43　(D)54　(E)1
(2002AMC12，http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1363532)


11.
等腰梯形ABCD，AB=CD=AD=6，AD平行BC，則梯形ABCD的最大面積為多少？
(A)272 　(B)273 　(C)276 　(D)213 　(E)216 
(我的教甄準備之路－用算幾不等式解三角函數的極值，https://math.pro/db/viewthread.php?tid=661&page=1#pid1077)


12.
設直線x=k與y=log5x、y=log5(x+4)分別相交，且已知兩交點的距離為0.5，若k=a+b ，其中a、b均為正整數，則a+b=？
(A)6　(B)7　(C)8　(D)9　(E)10
(1997AHSME，http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1379867)


13.
將5個A、5個B以及5個C等15個字母排成一列，使得前5個字母沒有A，中間5個字母沒有B，且最後5個字母沒有C，試問共有多少可能的排列？
(A)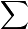5k=0[Ck5]3 　(B)3525　(C)215　(D)15!(5!)3　(E)315
(2003AMC12，https://math.pro/db/thread-454-1-1.html)

選擇題第九題
試問滿足m3+n3+99mn=333且mn0之序對(mn)有幾組整數解？(A)2　(B)3　(C)33　(D)35　(E)99
[解答]
①
(m+n)3=m3+n3+3mn(m+n)

⇒m3+n3=(m+n)3−3mn(m+n)
②
(m+n)3−3mn(m+n)−333−3(−33)mn=0

⇒(m+n−33)((m+n)2+(m+n)(33)+332)−3mn(m+n−33)=0

⇒(m+n−33)m2+2mn+n2+33m+33n+332−3mn=0

⇒21(m+n−33)2m2−2mn+2n2+66m+66n+2(33)2=0

⇒21(m+n−33)(m−n)2+(m+33)2+(n+33)2=0

⇒m+n=33有34組　或　m=n且m=−33且n=−33有1組

共35組

試問滿足m3+n3+99mn=333且mn0的序對(mn)有　　　組整數解。
(110臺南女中，https://math.pro/db/viewthread.php?tid=3503&page=1#pid22511)

若mn為整數且mn0，則滿足m3+n3+93mn=313的整數數對(mn)有　　　組。
(110高中數學能力競賽北一區筆試二，https://math.pro/db/thread-3612-1-1.html)

113.6.17補充
設m、n為整數，且mn0，則滿足m3+n3+93mn=313的序對(mn)有多少組？
(113花蓮女中，https://math.pro/db/thread-3889-1-1.html)

引用:

原帖由 shingjay176 於 2014-4-11 07:48 AM 發表
選擇題第九題

a^3+b^3+c^3-3abc=(1/2)*(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]-------------(*)
又m^3+n^3+99mn=33^3
改成m^3+n^3+(-33)^3-3mn(-33)
令a=m,b=n,c=-33代入(*)

選擇題第四題

K=0 跟 K=2003 帶入是一樣的（同界角），

若 Z=0，會有 2003 組。

另外，還有一組則是 (ab)=(00)



一樣做法，但換個寫法再寫一次～

選擇題第 4 題：

令 Z=a+bi，依題意 Z2002=Z

　　Z2002=ZZ2002=ZZ=0 或 Z=1

case i: 若 Z=0，則 (ab)=(00)

case ii: 若 Z=1，則 Z2002=1ZZ2003=1

　　　　Z=cos2k2003+isin2k2003 ，其中 k=01232002

　　　　(ab)=(cos2k2003sin2k2003)，其中 k=01232002

故，所求共有 1+2003=2004 組。

QQ.GIF (25.23 KB)

2014-4-15 10:59

(1) z101=z 非多項式方程式。代數基本定理不適用

(2) 是，根據代數基本定理 z102=1 有 102 個根。但代數基本定理不保證這些根滿足 z=1

(3) z102=zz  單看此方程式，z=0 的確是一個解，但原本的方程式 z101=z 就有此解，故無增減根問題(非多項式方程式，無重根問題)。

但在 (3) 中 z102=1 實際上是 z102=zz 、 z=1 聯立的結果

也就是利用 z=1 進行化簡，在此前提下，z=0 ，因此此例中並沒有增根。反而是因多一個限制條件 z=1

使得 z102=1 的解的個數比 z101=z 還少一個

(4) 同(3)