想請問第5，6，7，8，12，13，15題，
順便請問有沒有人有算答案(想對答案)，謝謝!

第 5 題

a1a2a2013 為 0 或 −1k2n  其中 k12n0122013

因此共有 1+22014=4029 種可能值。



第 6 題：

以邊長 72015 做三角形，

所求＝在邊長 7 上的對應高長＝7227+20+152−7+20+1527−20+1527+20−15=12 

ps. 如有計算錯誤，還請告知，感謝。

第 7 題：

令圓半徑為 R，

在 ABD 中，由正弦定理，

可得 BDsin+=2RR=52 


因為 AC 為直徑，所以 ABC=ADC=90 

ABC面積=R2sin2ADC面積=R2sin2

因為 ABC面積=2ADC面積

可得 sin2=2sin2 ‧‧‧（＊）

因為 +=45，所以 2=90−2

sin2=cos2 ‧‧‧（＊＊）

由 （＊）＆（＊＊），可知 cos2=21sin2

帶入 sin22+cos22=1

sin22+21sin22=1 

sin2=25

（因為 0290 ，所以 sin2 為正數）

ABC面積=R2sin2=205 

註：感謝 寸絲老師 提醒小錯誤，已更正。 ：）

第 8 題：

設 CD 直線方程式為 x+2y−k=0

四條直線兩兩解二元一次聯立方程式，

可得 A(3−1)B(10)C(34−k32k−2)D(5k+1452k−7)

再帶多邊形面積公式（測量師公式，或是要把它拆成 ABC+ADC 也可以）

3−11034−k32k−25k+1452k−73−1=45

可解得 k 之值，進而得  CD 直線方程式。

第七題，不解釋

第 12 題：

設 L 的方向向量 v=(7−8−11)

　 平面 2x−y+2z=0 的法向量 n=(2−12)

已知 L 通過 A(2−12)，

先求得 A 在 E 上的投影點為 A1(000)

設 A 在題目要求的直線上的投影點為 A2

則 AA1=3A1A2=35−32=26 

向量 A1A2=26nvnv 

然後可得 A2 點坐標，再加上 L 直線的方向向量 v

進而得知題目所求知直線方程式。

如看不懂，請參考下圖：

2013-11-01 11.55.12.jpg (77.71 KB)

2013-11-1 11:59

第 10 題：

2013-11-01 12.17.48.jpg (112.67 KB)

2013-11-1 12:27

第 7 題，面積是 R2sin2 才是吧?

順帶提供一些答案，隨手亂寫的，應該不少錯誤

1. 16 (thepiano 兄的答案才正確，更正之)
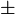2. a=11b=−14c=1d=1 (thepiano 兄的答案才正確，更正之)
3. 71
4. 32 
5. 4029
6. 12
7. 205 
8. x+2y−16=0 (感謝 thepiano 提醒)
9. 30
10. k=1 拋物線；k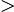1 橢圓；0k1 雙曲線。(先前看反，thepiano 大的答案才正確，已更正之 2013.09.08)
11. \frac{175}{459}
12 \frac{x-3}{7}=\frac{y-4}{-8}=\frac{z+1}{-11} ，或 \frac{x+3}{7}=\frac{y+4}{-8}=\frac{z-1}{-11} (漏了負號，已補上，感謝 thepiano 更正)

14. AC
15. AC
16 \frac{165}{4} (與 thepiano 相同 2013.09.08補充)
17. 20
18.   \frac{1}{\sqrt{5}}\left[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}\right]

[ 本帖最後由 tsusy 於 2013-9-8 09:25 PM 編輯 ]

有幾題跟 寸絲 兄有點出入，請大家幫忙驗證一下
(1) 16
(2) d = ±1
(10) 0 ＜ k ＜ 1 是雙曲線，k ＞ 1 是橢圓
(12) 分母 -8
(16) 165/4

話說，代理教師考這麼多題，會不會有點狠？

[ 本帖最後由 thepiano 於 2013-7-19 10:07 PM 編輯 ]

第 13 題：

\overleftrightarrow{CD} 直線斜率＝\displaystyle \frac{1}{t}

\Rightarrow \overleftrightarrow{CD} 直線方程式為 \displaystyle y=\frac{1}{t}x-1

上式與 x+y=1 解聯立方程式，

求得 \displaystyle D(\frac{2t}{1+t}, \frac{1-t}{1+t})

\displaystyle \Rightarrow \triangle BCD \mbox{面積}=\frac{1}{2}\cdot1\cdot1-\frac{1}{2}\cdot1\cdot t-\frac{1}{2}\cdot(1-t)\cdot\frac{1-t}{1+t}=\frac{t-t^2}{t+1}

令 \displaystyle k=\frac{t-t^2}{1+t}

\displaystyle \Rightarrow t^2+\left(k-1\right)t+k=0

因為 t\in\mathbb{R}，所以 \left(k-1\right)^2-4\cdot1\cdot k\geq0

\Rightarrow k\geq3+2\sqrt{2} 或 k\leq 3-2\sqrt{2}

且因為 \displaystyle k\leq\triangle OAB\mbox{面積}=\frac{1}{2}

可得 \displaystyle k\leq3-2\sqrt{2}

當 k=3-2\sqrt{2} 時，帶入 t^2+\left(k-1\right)t+k=0

可解得 t=\sqrt{2}-1

因此，(\alpha,S)=(\sqrt{2}-1, 3-2\sqrt{2})

更狠的是全部都是計算題，都要過程

連多選題也要理由