有鑑於學校沒公告數學科的試題

所以來回憶一下題目，有的地方沒有記得很清楚

還請有考試的考生幫忙回憶一下，謝謝！部分題目可能不太正確

其中填5 的圖是自己畫的，跟試卷的標記可能不太一樣，也忘了要求哪段的長度了

填10，則是只記得形狀，忘記數字了，經 Google 大神協助本題出處應為 2004年(第三屆)中國女子數學奧林匹克試題
數字為 a+3ca+2b+c+4ba+b+2c−8ca+b+3c

填11，敘述也許和原題有出入?因為題目寫得太長了

另外填12，題目是否有給 x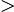−1 之類的條件？

請慢慢享用

附上部分個人算的數字，僅供參考，歡迎指正。

填充題
1. −160159                     2. 25b4

3. 132                         4. 2084

5. 21+43−3           6. 611

7. 110                       8. 54

9. x21−5  或 1x21+5 

10. −17+122        11.n−1

12. 1x+1

計算3. (00z) 及 (1−1−1)

附件檔案修正
2. 修正填 2 的敘述，感謝鋼琴大修正。
3. 補上漏掉的條件 f(6x)=2f(x)，感謝鋼琴大提醒。
5. 應該求 BE 之長。
8. 修正為 bx2，感謝 dream10 提醒修正。
12. 修正為 tx

6.空間中，有四個球兩兩相切(外切)，半徑分別為2,3,2,3。有另一球與四球外切，則其半徑=？

空間有四個球，他們的半徑分別為2,2,3,3，每個球都與其餘3個球外切，另有一個小球與那四個球都外切，求該小球的半徑？
(1995中國數學奧林匹克)

102.4.14補充
感謝老王提醒忘了還有索迪公式
計算3(122+122+132+132+1r2)=(21+21+31+31+r1)2
解出r=611−6
老王的部落格有證明h ttp://tw.myblog.yahoo.com/oldblack-wang/article?mid=5697&prev=5702&next=-1連結已失效
拼圖拼字拼數學P229，https://math.pro/db/viewthread.php?tid=836&page=1#pid1604



SketchUp檔下載

[ 本帖最後由 bugmens 於 2013-4-14 07:05 PM 編輯 ]

請教填充 9,2 有無什麼好方法

9.
不等式(x−1)32x2−4x+3x3+2x的實數解為　　　　。
[解答]
個人的想法是 LHS=2x−1+1(x−1)3 分段遞減。而且在 1 處為

而 RHS=x3+2x 微分可知，嚴格遞增。

故僅需解 (x−1)32x2−4x+3=x3+2x 之兩實根。

即方程式 x6−3x5+5x4−7x3+4x2+2x−3=0 之兩實根

而不等式之解則為 x1x。

但易驗，該六次式沒有理根，然後就卡了

附上 Wolfram Alpha 的答案 x21−5  或 1x21+5 

2.
平面上坐標上，為所有的點P滿足到直線x=4與(10)的距離和為5之曲線。試求b的範圍，使得上恰有三組點，關於點(b0)對稱。
[解答]
想法，先畫個概圖

pic.png (11.03 KB)

2013-4-14 09:28

注意上下對稱於 x 軸 必一組，另兩組為是 y=c，四個交點成矩形，畫個對角線交點就是 (b0)

但 c=0, b=25 會多出一組左右對稱點，隨著 c 從 04，猜測 b 從 254

故猜答案為 25b4

填充第 2 題
寸絲老師的幾何解法很漂亮且答案應是正確的，建議題目最後一句改成 "使得Γ上恰有三組點，關於(b，0)對稱" 比較好理解

這題最難的地方是畫出Γ

關於第六題
順便記一下索迪(Soddy)公式吧:
對於n維情況，有n+2個球互相切來切去，所有球的半徑記為 ri，
再記半徑的倒數為 ci=1ri
那麼有
nn+2i=1ci2=(n+2i=1ci)2 

我後悔了，本來打算不等式推推推出來，
推了半天推出錯
還是跟隨寸絲老大的腳步求那兩根就好
(x−1)32x2−4x+3=x3+2x
(x−1)32x2−4x+2−2x=x3−1(x−1)3
−2(x−1x−1)=(x−1x−1)(x2+xx−1+1(x−1)2)
x−1x−1=0
x=21+−5 
所以x21−5 或1x21+5 

解得漂亮，原來是把 2 跟 2 放一起，1 跟 1 也放一起

什麼時候我才可以也有這種眼力，看出其中竅門所在

有關填充 2，我發現 Γ 其實只是兩個拋物線的合成圖:
x4 時，為 y2=4xΓ1
x4 時，為 y2=−16x+80Γ2

不難得到若要在 Γ1上找一組點對稱 (b,0)，則這組點必對稱 x 軸。
所以要在兩個拋物線上各找一點，才有可能產生三組關於 (b,0) 的對稱點。

令 P(4a2a)，其關於 (b,0) 的對稱點 Q(2b−4a2−a) 落在 Γ2 上，
化簡得到 b=323a2+80
因為 0a4，故 25b4。

別誇我 , 我寧願拿我碰巧的眼力換你千錘百鍊的實力
小弟正在算你的大作        Math Note 01-10
目前正在第九頁 , 看到了一些錯誤 , 不過可以肯定的是數學寶典不會再是101了
被你奪走了
對了
42題 , 我弄不出來

原來如此~~感謝 Joy091 解惑

另外填 3 是個有趣的題目，做法如下

填 3.
若函數f(x)滿足f(1)=1，f(x)+f(1−x)=1，x6=21f(x)，其中0x1，且對0x1x21，有f(x1)f(x2)，則f(12013)=　　　。
[解答]
注意由函數之性質可得 f(61)=21=f(65)

又 6164201365, 故 f(642013)=21

因此所求 f(12013)=132

補充一類題：設函數 f(x) 在1x  3 時，滿足 f(x)=1−x−2 ，且對所有的正數 x，f(x) 滿足f(3x)=3f(x)。試求最小的正數 x 使得 f(x)=f(2011)。
(100二區能力競賽 )(2001AIME 則是 2011變成 2001)

填 4.
2013k=15k2013= 　　　。([]為高斯符號)
[解答]
則是基本的題型，提供一個有趣的方法：Fubini 定理

令 S=5k2013k=1232013 , Sn=Sxxn。

由 Fubini 定理有 \sum\limits _{k=1}^{2013}\left[\sqrt[5]{\frac{2013}{k}}\right]=\sum\limits _{n=1}^{\infty}|S_{n}| 。

\left[\sqrt[5]{\frac{2013}{k}}\right]\geq n\Leftrightarrow\frac{2013}{k}\geq n^{5}\Leftrightarrow\frac{2013}{n^{5}}\geq k ，

故 |S_{n}|=\left[\frac{2013}{n^{5}}\right]=2013,62,8,1,0,0\ldots 。故所求 =2013+62+8+1=2084。

類題：2. y=[x] 表高斯函數，求 \sum\limits _{k=1}^{40}\left[10^{\frac{k}{40}}\right]。(101文華高中)