填充 4. 兩邊同時對 y 偏微得

f(x+y)=2f(x)f(y), y=0 代入得

f(x)=2f(x)f(0)=4f(x)f(x)f(x)=4

再來補充個類題，把原題取個 log 就很像下面的類題了

100 中壢高中1招填充 8. 設 fg 為可微分函數, 且 f(x+2y)=f(x)+g(y), xyR. 試問：若 f(0)=1, f(0)=2, 求 g(5).

看到這個類題後，聯想到第一次看到這個題型時，條件其實給的比較少：微分的條件，只要求 f 在 0 處可微，但從這個條件可以推出其它地方也可以微

不過，對於填充題的作答是沒什麼影響，如果是計算題就要小心條件了

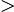現在把條件弱化一下，改成「 f(x+y)=2f(x)f(y) 對任意實數 xy 且 f(0)0f(0)=2」

也就是可微函數的條件和函數皆正被拿掉了，但我們還是可以小心地處理

令 x=y=0 代入解得 f(0)=21

若 y=0,  則 yf(x+y)−f(x)=y2f(x)f(y)−f(x)=2f(x)yf(y)−21

取極限y0, 得 f(x) 存在且 f(x)=2f(x)f(0)

現在只差把 f(x) 除過去，就結束了，所以需要 f(x)=0

若 0=f(x)=2(f(2x))2  ，也就是說 f(x)=0f(2x)=0f(x2n)=0

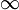
n 又 0 點處連續(可微必連續) 得 f(0)=0 矛盾，所以 f(x)=0

所以即使把條件弱化到只有 0 處局部的訊息，還是一樣的結果 f(x)f(x)=4

更甚者，可以直接把 f 算出來 f(x)=21ef(0)x, 其實就是解微分方程

引用:

原帖由 老王 於 2012-5-31 10:14 PM 發表
前天她問我的時候，一開始我也以為是要相切；但是又想一下，覺得不必。
後來實際去做的時候，就將直線y=kx+b代入拋物線和圓的時候，得到兩個方程式:
kx2−kx−b=0
(1+k2)x2−2ax−b2 ...

多謝老王老師的指教，將題目的意思看清楚看來也是一個值得學習的關鍵，長知識了～

在現場中  有考慮同時將三角形ABP及PBC逆時針旋轉90度來想ˇˇˇ並想利用餘弦定理來想

引用:

原帖由 weiye 於 2012-6-1 08:48 AM 發表
填充第 7 題，換個方向旋轉也不錯。

填充第 7 題，另解一：

1171

如圖，將 PBC 以 B 為旋轉中心，逆時針旋轉 90，

則 PQB 為等腰直角三角形，得 PQ=52 ，...

謝謝瑋岳老師

這個圖我看懂了

我記得建中通訊解得有類似題

昨天有去找,可惜沒找到

謝謝你

那再來一個另解好了，

填充第 7 題，

qq2.png (6.44 KB)

2012-6-1 20:28

如上圖，連接 PD，

因為 PA2+PC2=PB2+PD2

（上面這行用一堆畢氏定理就可以證出來了～）

可得 PD=5

因此，ABPADP 且 CBPCDP 　（兩者皆用ＳＳＳ全等性質）

可得 APC 三點共線，因此正方形 ABCD 的對角線 AC=7+1=8

可得正方形 ABCD 的邊長與面積。

引用:

原帖由 zeratulok 於 2012-5-29 07:52 AM 發表


第5可以用轉換的！
把[sin(2t-45),cos(2t-45)]轉換成[cos(135-2t),sin(135-2t)]
然後就可以算出他的範圍就在單位圓上的75～105度
接下來就看附圖應該就會了！
粗線就是p的移動軌跡（其實是沒有畫好....） ...

請問為什麼不可直接算[sin(2t-45),cos(2t-45)]　　
當ｔ=１５度,可得[sin(-１５度),cos(-１５度)]
當ｔ=３０度,可得[sin(１５度),cos(１５度)]

[ 本帖最後由 mandy 於 2012-6-1 10:24 PM 編輯 ]

引用:

原帖由 mandy 於 2012-6-1 10:20 PM 發表
請問為什麼不可直接算[sin(2t-45),cos(2t-45)]　　
當ｔ=１５度,可得[sin(-１５度),cos(-１５度)]
當ｔ=３０度,可得[sin(１５度),cos(１５度)]

可以呀， 畫出來還會是跟 #11 zeratulok 的圖一樣呀，

點 (cossin) 是位在單位圓上，從正向 x 軸開始逆時針旋轉 角，如下～

qq1.png (15.63 KB)

2012-6-1 23:18

而點 (sincos) 是位在單位圓上，從正向 y 軸開始順時針旋轉 角而已，如下～

qq2.png (15.27 KB)

2012-6-1 23:18

所以，[sin(-１５度),cos(-１５度)]～角度增加到～[sin(１５度),cos(１５度)]的點移動軌跡如下，

qq3.png (13.21 KB)

2012-6-1 23:25

引用:

原帖由 tsusy 於 2012-5-28 11:01 PM 發表
填充 9. 小弟來個暴力解，應該有其它比較優的方法

坐標化 C(00)A(0a)B(0b), 向量全寫下了

內積和除以 n 列式得 1nnk=1n2k(k−1)(a2+b2)

可 ...

ＡＢＣ是直角三角形,Ｂ座標是不是(ｂ,０),若用(ｂ,０)做,　內積和的列式裡係數就會有ｎ　?

請問版上的老師第六題該怎麼做啊?

祝各位老師   新年快樂!

填充題第 6 題：

法一：用排容原理，

8!−C237!2−6!3!−7!2−7!2 

　+C236!22−5!3!2+C236!22−5!3!2+6!22 

　−C235!222−4!3!22 

　=9216

任排－甲乙丙至少有兩人相鄰（三人同時相鄰有多扣要回補）－丁戊相鄰－己庚相鄰

　＋甲乙丙至少有兩人相鄰（三人同時相鄰有多扣要回補）且丁戊相鄰＋甲乙丙至少有兩人相臨（三人同時相鄰有多扣要回補）且己庚相鄰

　＋丁戊相鄰且己庚相鄰

　－甲乙丙至少有兩人相鄰（三人同時相鄰有多扣要回補）且丁戊相鄰且己庚相鄰

法二：先分類之後列出 "丁戊己庚辛" 的排列方法，

　　　分類方式是按照丁戊、幾庚這兩組分成

　　　"1. 兩組都相鄰（3!22=24） 2. 兩組恰一組相鄰（C124!2−24=48 ） 3. 兩組都沒有相鄰（5!−24−48=48）"，

　　　然後再讓甲乙丙插空隙。

　　　24324+48354+48654=9216 

類題：https://math.pro/db/thread-1610-1-1.html