空間中,四面體
A−BCD,
AB=CD=6,
AC=AD=BC=5,
BD=7,求四面體
A−BCD的體積為
。
[解答]
我發現用內積也滿好算的!
令 A(0,0,0), B(6,0,0), C(3,4,0), D(x,y,z)
則有
x2+y2+z2=25

 (1)
18=−−
(1)
18=−− DA
DA −−
−− DC=(−x
DC=(−x −y
−y −z)
−z) (3−x
(3−x 4−y
4−y −z)
19=−−
−z)
19=−− DA
DA −−
−− DB=(−x
DB=(−x −y
−y −z)
−z) (6−x
(6−x −y
−y −z)
x(x−3)+y(y−4)+z2=18
−z)
x(x−3)+y(y−4)+z2=18

 (2)
x(x−6)+y2+z2=19
(2)
x(x−6)+y2+z2=19

 (3)
(3)
(1) 代入(3) 可得
x(x−6)+25−x2=19, 解出
x=1 代回
可得
y2+z2=24 與
y(y−4)+z2=20, 再解出
y=1
於是
z=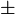
 23
23
可取
−− AD=(1
AD=(1 1
1
 23)
23)
所以四面體 A-BCD 體積為
61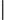
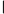
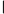
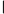
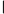
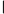
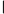 163104
163104 23 0 0
23 0 0 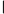
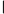
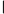
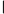
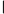
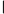
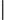 =4
=4 23
23