14.
已知空間坐標中,
A( 3
3 1
1 2
2 3)
3) ,
B(2 2
2 3
3 8)
8) ,
P點為
L1:
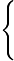 x−
x− 3y=0z=0
3y=0z=0 上的任一點,
Q點為
L2:
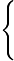
 3x−y=0z=0
3x−y=0z=0 上的任一點,試求
AP+PQ+QB的最小值。(輔教12-2例題9改編)
15.
數學科辦公室有一個正方形窗戶,辦公室內的天花板的電燈(假設為一個點光源)透過窗戶在地板上形成一個四邊形的光影,令假設以地板為
xy平面,建立一個空間直角坐標系(已知窗戶所在的牆壁面與地板垂直,而且窗戶的邊框分別與地板平行或垂直),發現窗戶光影外框的四個頂點坐標分別為
A(6 10
10 0)
0) B(8
B(8 14
14 0)
0) C(−4
C(−4 23
23 0)
0)以及
D(−2 16
16 0)
0),試求電燈光源的坐標。(輔教12-2例題8改編)