\( f(x) = x^2 +bx +c \)，\( f(f(x)) ? =0 ? \) 恰有三實根

看來有點怪，如果 b,c 皆實數，\( f(f(x)) \) 是實係數四次多項式，虛根共軛成雙，不可能恰三實根

橢圓這題可以走海龍公式。

令 \( d = \overline{AF_1}, e = \overline{BF_1}, f = \overline{AB} = d + e  \)

首先由 \( \angle AF_1F_2 + \angle BF_1F_2 = 180^\circ \) 及餘弦定理可得 \( \frac{d+e}{de} = \frac{9}{16} \Rightarrow de = \frac{16}{9}f\)

由海龍公式有 \( 32 = \triangle ABF_2 = \sqrt{18\cdot(18-d-e)de} = \sqrt{32(18-f)f} \)

平方可解得 \( f = 16 \) 或 2 (不合)

正方形面積，見下圖

pic.png (44.82 KB)

2015-5-4 23:28

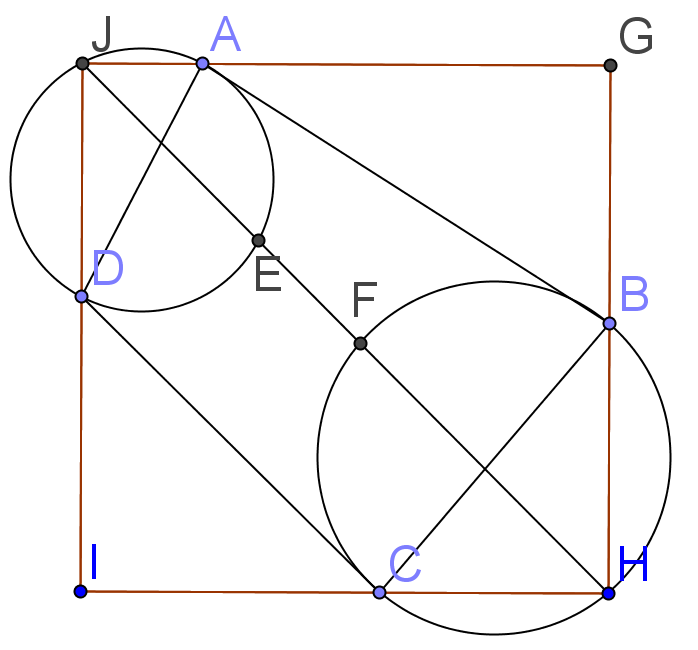
JH 為正方形對角線，故 \( \angle AJE = 45^\circ = \angle BHF \)

故 E, F 分別為半圓 AED, BFC 之中點(也在 AD, BC 中垂線上)

計算可得 \( E(\frac{1}{2},\frac{15}{2}) \), \( F(\frac{9}{2},\frac{11}{2}) \) (使用 1樓數據)

故對角線的方程式為 \( x+2y=\frac{31}{2} \)

與兩圓方程式分別解聯立可得正方形對角線上的一組頂點 \( J(-\frac{51}{10},\frac{103}{10}), H(\frac{25}{2},\frac{3}{2}) \)

正方形面積 \( \frac12 \overline{JH}^2 = \frac{968}{5} \)

歪線那題  忘了在哪份考古題做過類似題了，

為了方便，先做一個轉換，空間中任意點沿著 \( L_2 \) 的方向移動時，點和直線 \( L_2 \) 的距離保持不變。

將 \( A, C \) 沿著 \( L_2 \) 的方向移動至 \( A', C' \) 使得 \( \vec{BA'}, \vec{BC'} \) 和 \( L_2 \) 的方向向量垂直。

移動後 \( A', B, C' \) 的點仍共線，且 \( \overline{A'B}:\overline{BC'} = 2:1 \)，保持原比例。

同樣的，可以移動 \( L_1 \) 上的每個點，使得移動後所得 \( L' \) 過 B，其方向與 \( L_2 \) 方向垂直，且各點至 \( L_2 \) 的距離仍不變。

坐標化，以 \( B \) 為原點，\( \vec{BC} \) 方向為正 x 軸，\( L_2 \) 方向為 z 軸。

令 \( A'(-2x,0,0), B(0,0,0), C(x,0,0) \), \( L_2 :\begin{cases}
x= & a\\
y= & d
\end{cases} \)，其中 \( x>0 \)

計算距離得 \( \begin{cases}
(a+2x)^{2}+d^{2} & =33\\
a^{2}+d^{2} & =9\\
(a-x)^{2}+d^{2} & =24
\end{cases} \)

\( \Rightarrow\begin{cases}
4ax+4x^{2} & =24\\
-2ax+x^{2} & =15
\end{cases}\Rightarrow6x^{2}=54\Rightarrow x=\pm3 \)

\( x =3 \Rightarrow a=-1 \Rightarrow d^2 =8 \)

所求歪斜距離 \( d(L_1,L_2) = d(L',L_2) = \sqrt{8} = 2\sqrt{2} \)

第13題. 上次好像在書上看過，做一下，應該是這樣吧

(1) 若 \( A = \{ 2014,2015,\ldots, 4028 \} \) 為 2014~4028 的 2015 個連續正整數所組成集合。其中任兩個元素的和 \( \geq 4029 \)，故此 \( A \) 滿足題意。故 \( M \) 的最小值 \( \leq 4028 \)

(2) 若有另一個 \( A \) 為滿足題意且 \( M = \max{A} \leq 4028 \)。

考慮 \( B_k = \{ k,M-k \} \), \( k = 1,2,3,\ldots, [\frac M2] \)。

因 \( k + (M- k) = M \)，故每一個 \( B_k \) 中至多一個數屬於 \( A \)，故 \( n(A) \leq 1 + [\frac M2] \leq 1 + \frac{4028}{2} =2015 \)

又 \( n(A) = 2015 \)，因此上式的不等式其實為等式，又 \( M \leq 4028 \)，故 \( M =4028 \)。

綜合 (1)(2) 得 \( M \) 的最小值為 4028

[ 本帖最後由 tsusy 於 2015-6-28 08:51 PM 編輯 ]

那看看奧數教程裡的寫法好了

pic.png (51.76 KB)

2015-7-2 22:02