選擇第 1 題:
已知空間中三直線\(L_1\):\(\displaystyle \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\),\(L_2\):\(\displaystyle \frac{x-2}{-2}=\frac{y-4}{-3}=\frac{z}{1}\),\(L_3\):\(\displaystyle \frac{x-3}{2}=\frac{y-2}{1}=\frac{z-1}{3}\),下列何者可能為此三直線投影到\(xy\)平面的圖形?
分析:空間中,一點 \(P(x_0,y_0,z_0)\) 滿足關係式 \(\displaystyle \frac{x_0-x_1}{a}=\frac{y_0-y_1}{b}=\frac{z_0-z_1}{c}\)
則 \(P\) 投影到 \(xy\) 平面之後,投影點為 \(Q(x_0,y_0,0)\),
當然 \(x_0, y_0\) 還是滿足關係式 \(\displaystyle \frac{x_0-x_1}{a}=\frac{y_0-y_1}{b}\)
解答:
畫出 \(xy\) 平面上的三條直線 \(\displaystyle \frac{x-1}{2}=\frac{y-2}{3}, \frac{x-2}{-2}=\frac{y-4}{-3},\frac{x-3}{2}=\frac{y-2}{1}\) 即可得所求圖形。
前兩條互相平行,第三條不與前兩條平行。
選擇第 6 題的第五個選項:
三次函數\(\displaystyle f(x)=\frac{1}{3}x^3-x\)之圖形為曲線\(\Gamma\),由點\(\displaystyle A(2,-\frac{2}{3})\)作曲線\(\Gamma\)的切線,則下列敘述何者為真?
(1)其中有一切線的切點其\(x\)座標為1
(2)由點\(A\)可作三相異切線
(3)其中有一切線的斜率是0
(4)所有切線的斜率和為6
(5)其中有一切線與曲線\(\Gamma\)有2個相異交點
圖形如下圖,

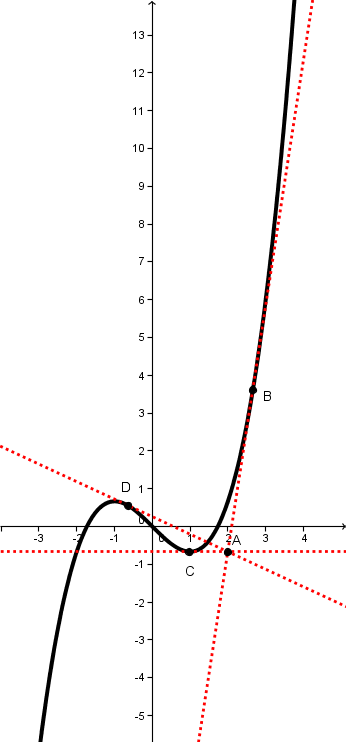
畫的清楚的話應該就可以看出答案了,
也可以麻煩一點~解切點、切線、再與 \(\displaystyle y=\frac{1}{3}x^3-x\) 解交點。==
選擇第 8 題:
已知方程組\((A)\):\(\cases{a_1x+b_1y+c_1z=d_1 \cr a_2x+b_2y+c_2z=d_2 \cr a_3x+b_3y+c_3z=d_3}\)及方程組\((B)\):\(\cases{a_1x+b_1y+c_1z=0\cr a_2x+b_2y+c_2z=0\cr a_3x+b_3y+c_3z=0}\),
設\((1,2,3)\)及\((10,-1,9)\)均為方程組\((A)\)的解,則下列敘述何者為真?
(1)方程組\((A)\)的幾何意義為三平面交於一直線
(2)方程組\((B)\)恰有一組解\((0,0,0)\)
(3)方程組\((B)\)有無限多組解
(4)\((300,-100,200)\)為方程組\((B)\)的一組解
(5)\((1,2,3)\)為方程組\((B)\)的一組解
[解答]
令 \(P(1,2,3), Q(10,-1,9)\),則
選項(1):方程組(A)可能為直線 \(PQ\) 或包含直線 \(PQ\) 的某一個平面。
選項(2):方程組(B)可能為通過原點且平行於直線 \(PQ\)的直線,
或通過原點且平行於直線\(PQ\)的平面。
亦即,方程組(B)有無限多組解且通過 \((0,0,0)\)。
選項(3):承選項(2),正確。
選項(4):承選項(2),方程組(B)的圖形至少包含直線 \(\displaystyle \frac{x-0}{9}=\frac{y-0}{-3}=\frac{z-0}{6}\)
且點 \((300,-100,200)\) 在上述直線上,故 \((300,-100,200)\) 為方程組(B)的一組解。
選項(5):承選項(3),直線 \(\displaystyle \frac{x-0}{9}=\frac{y-0}{-3}=\frac{z-0}{6}\) 並不包含點 \((1,2,3)\)
因此無法保證方程組(B)(其圖形可能為直線或平面)有解 \((1,2,3)\)。
填充第 18 題:
已知\(x\ge 0\),\(y\ge 0\),\(z\ge 0\)且\(2x+y+z=4\),若\(x+3y\le5\),則\(x+y\)的最大值為
。
[解答]
\(z=4-2x-y\geq 0\)
線性規劃,先畫出可行解區域 \(\displaystyle \left\{\begin{array}{c}x\geq0,\\ y\geq0,\\ x+3y\leq 5, \\ 4-2x-y\geq0\end{array}\right.\)

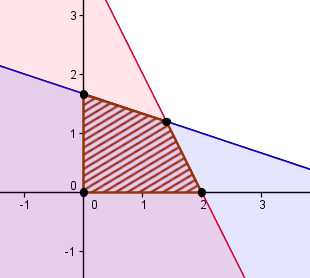
再找出可行解區域的頂點,然後帶入限制條件 \(x+y\),然後找出最大值。
填充第 14 題:
在\(\Delta ABC\)中三內角為\(∠A\)、\(∠B\)、\(∠C\),已知\(4sinB+3cosC=1\)、\(3sinC+4cosB=6\),則\(∠A\)的度數為
。
[解答]
\(4\sin B+3\cos C=1\)、\(3\sin C+4\cos B=6\) 兩式平方後相加,
可得 \(\displaystyle \sin(B+C)=\frac{1}{2}\Rightarrow B+C=30^\circ\) 或 \(150^\circ\)
若 \(B+C=30^\circ\),則 \(0^\circ<B<30^\circ\) 且 \(0^\circ<C<30^\circ\)
\(\displaystyle \Rightarrow 0<\sin B< \frac{1}{2}, \frac{\sqrt{3}}{2}< \cos C< 1\)
\(\displaystyle \Rightarrow 4\sin B+3\cos C>4\times 0 + 3\times \frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}\)
此與 \(4\sin B+3\cos C=1\) 相矛盾,不合。
\(B+C=150^\circ\Rightarrow A=30^\circ\)