題號不一定按照順序 還請有去的老師一起補完

1.絕對值函數=a有三實根，求a的範圍
2.一個6*1的方格用紅黃綠三種顏色塗，每格塗一種顏色，規定3種顏色至少要都用到一次，問紅色不相鄰的情形有幾種
3.一個正五邊形ABCDE，\(\vec{AC}\)=\(x\vec{AB}\)+\(y\vec{AE}\) 求\((x，y)\)
4. \(2x^3-x \)= \(cos(10\pi x)\)有幾個實根
5.\(\Delta ABC\) ，\(\overline{AB}=5\)。\(\overline{BC}=7\)。\(\overline{AC}=6\) ，\(B\)點對\(\overline{AC}\)做垂線交\(\overline{AC}\)於\(E\)點，\(C\)點對\(\overline{AB}\)做垂線交\(\overline{AB}\)於\(F\)點
求\(\overline{EF}\)

6.
7.\(\displaystyle \lim_{n\rightarrow\infty } \sum_{k=1}^{n}\frac{1}{n!+(n+1!)}\)

8.(1) .a。b，c屬於實數，求\(4a+4b+4c-a^2-b^2-c^2\)的最大值
   (2)\(\displaystyle 2^{\frac{a}{2}+\frac{2}{b}}\)+\(2^{\frac{b}{2}+\frac{2}{c}}\)+\(2^{\frac{c}{2}+\frac{2}{a}}\)的最小值
   (3)若\(\displaystyle\frac{a}{2}+\frac{2}{b}\)=\({log_{2}}^{4b-a^2}\)，\(\displaystyle\frac{b}{2}+\frac{2}{c}\)=\({log_{2}}^{4c-b^2}\)，\(\displaystyle\frac{c}{2}+\frac{2}{a}\)=\({log_{2}}^{4a-c^2}\)，求\(a，b，c\)

想請問 2 .3. 8(2)(3)

2.知道怎麼算了XD
分三種情形
1個紅球：不管怎麼選一定不相鄰 剩下的方法數為2^5-2 共有180種
2個紅球：不相鄰的情形有10種 剩下的方法數為2^4-2 共有140種
3個紅球：不相鄰的情形有4種 剩下的方法數為2^3-2，共有24種
總和為344種

我印象中題目就是這樣
如果題目改成都是正實數該如何下手?

順便補一下中午想到的做法

66581960_2407227336264285_4519691796086784000_n.jpg (40.26 KB)

2019-7-7 20:57

2021.7.15新增
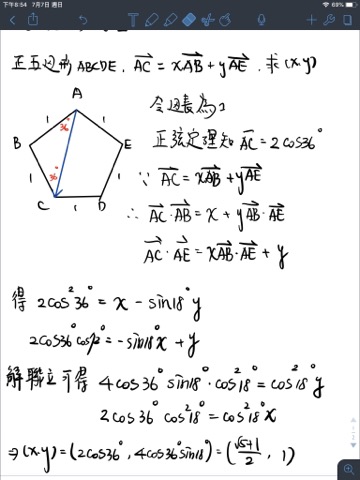
設\(\displaystyle \overline{BE},\overline{AC}\)交點為\(F\)，\(\overline{BF}:\overline{FE}=x:y\)
令\(\displaystyle \vec{AF}=y\vec{AB}+x\vec{AE}\)，且\(\overline{AF}:\overline{FC}=x:y\)
可得\(\displaystyle \vec{AC}=\frac{y}{x}\vec{AB}+\vec{AE}\)

又\(\displaystyle \overline{BF}=\frac{1}{2sin54^{\circ}},BE=2cos36^{\circ}\)

所以\(\displaystyle \overline{BF}:\overline{FE}=2 : (\sqrt{5}+1)\)

得\(\displaystyle \frac{y}{x}=\frac{\sqrt{5}+1}{2}\)