填充1
感謝laylay老師的說明，小弟另外再補充個作法
題意所求可視為7個區塊(傳7次)，5種不同顏色(人)，相鄰區域不同色，因為必須傳給Lin，故最後一個區域必須固定，故除5
\(
\displaystyle \frac{{(5-1)^7 +(-1)^7(5-1)}}{5} = 3276
\)

填充6 除了三角函數硬爆外，大家有其他想法嗎？

填充7  當A、D、P共線時周長最大


填充8  答案錯了，應該是\(-2\)


填充13
\(
\displaystyle 一路領先問題 \frac{{C_{51}^{99+51-1+2} +C_{51-1}^{99+51-1+2} }}{{C_{51}^{150} }} = \frac{{151}}{{202}}
\)


計算6
\(
\begin{array}{l}
\displaystyle \left( {\frac{{a^2 }}{{a+3b}}+\frac{{b^2 }}{{a+3b}}+\frac{{b^2 }}{{b+3c}}+\frac{{c^2 }}{{b+3c}}+\frac{{c^2 }}{{c+3a}}+\frac{{a^2 }}{{c+3a}}} \right)\left( {a+3b+a+3b+b+3c+b+ 3c+c+3a+c+3a} \right) \\
\displaystyle  \ge \left( {a + b + b + c + c + a} \right)^2  \\
\end{array}
\)

[ 本帖最後由 eyeready 於 2017-4-27 10:30 編輯 ]

請參閱
另想請教g112 兄 填充10 您是怎麼算的呢？

填充8
\(
己知線段\overline {AB} 是以C(0,1)為圓心且與函數y = \frac{1}{{|x|-1}}的圖形有交點
\)
\(
的所有圓中半徑最小的圓的一條直徑，O為原點，則向量OA\) \(\cdot \)\(向量 OB？\)

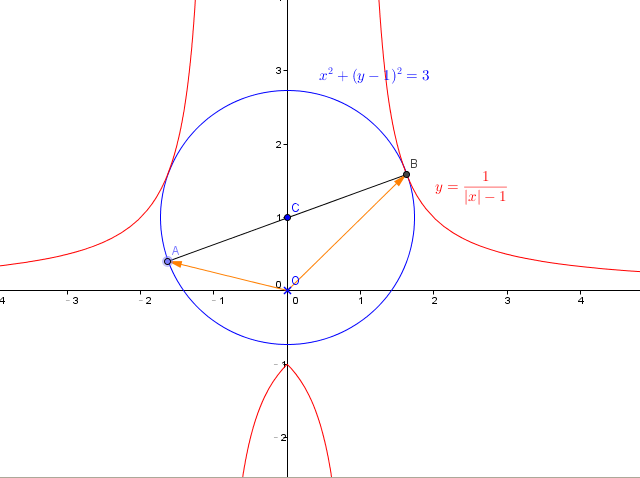
\(如上圖所示，最小圓發生於相切時，可用判別式等於0求得半徑之值\)
\(
取右半圓x>0，設x^2+(y-1)^2=r^2代入\displaystyle y = \frac{1}{{|x|-1}}
\)
\(
\begin{array}{l}
\displaystyle 可得r^2-(y-1)^2 = (\frac{1}{y}+1)^2整理完後得到
\displaystyle y^2-2y+2+\frac{2}{y}+\frac{1}{{y^2 }} =r^2
\end{array}
\)
\(
\displaystyle 再令t = y - \frac{1}{y},整理可得t^2-2t+4-r^2=0
\)
\(
因為最小圓相切恰一解，判別式=0，可得r^2=3，
可取A(0, - \sqrt 3+1)
\)
\(
B(0,\sqrt 3+1)求出所求為-2
(設參數式亦可)
\)

[ 本帖最後由 eyeready 於 2017-4-28 21:50 編輯 ]

第十題 小弟試著用GGB繪圖會比較直觀一些
PS：想請教各位老師們Case 1 有沒有比較快的討論法呢？


[解]
Case1：正四面體邊長為6的相交情況


Case2：正四面體邊長為6根號3的相交情況


[ 本帖最後由 eyeready 於 2017-5-10 17:51 編輯 ]

\(
\begin{array}{l}
\overline {AF}  + \overline {PF}  + \overline {PA}  = \overline {AF}  + \overline {PA}  + (2a - \overline {PD} ) \\
  = \overline {AF}  + 2a + \overline {PA}  - \overline {PD}  \le \overline {AF}  + 2a + \overline {AD}  \\
\end{array}
\)
可知當P、A、D共線時有最大值
PS：106新北聯招有出類似題

[ 本帖最後由 eyeready 於 2017-5-17 16:38 編輯 ]