回復 12# matric 的帖子
或許也能考慮直接用計算的方式:
利用算 catalan 數的觀念(對稱),直接計算不經過對角線的捷徑數:
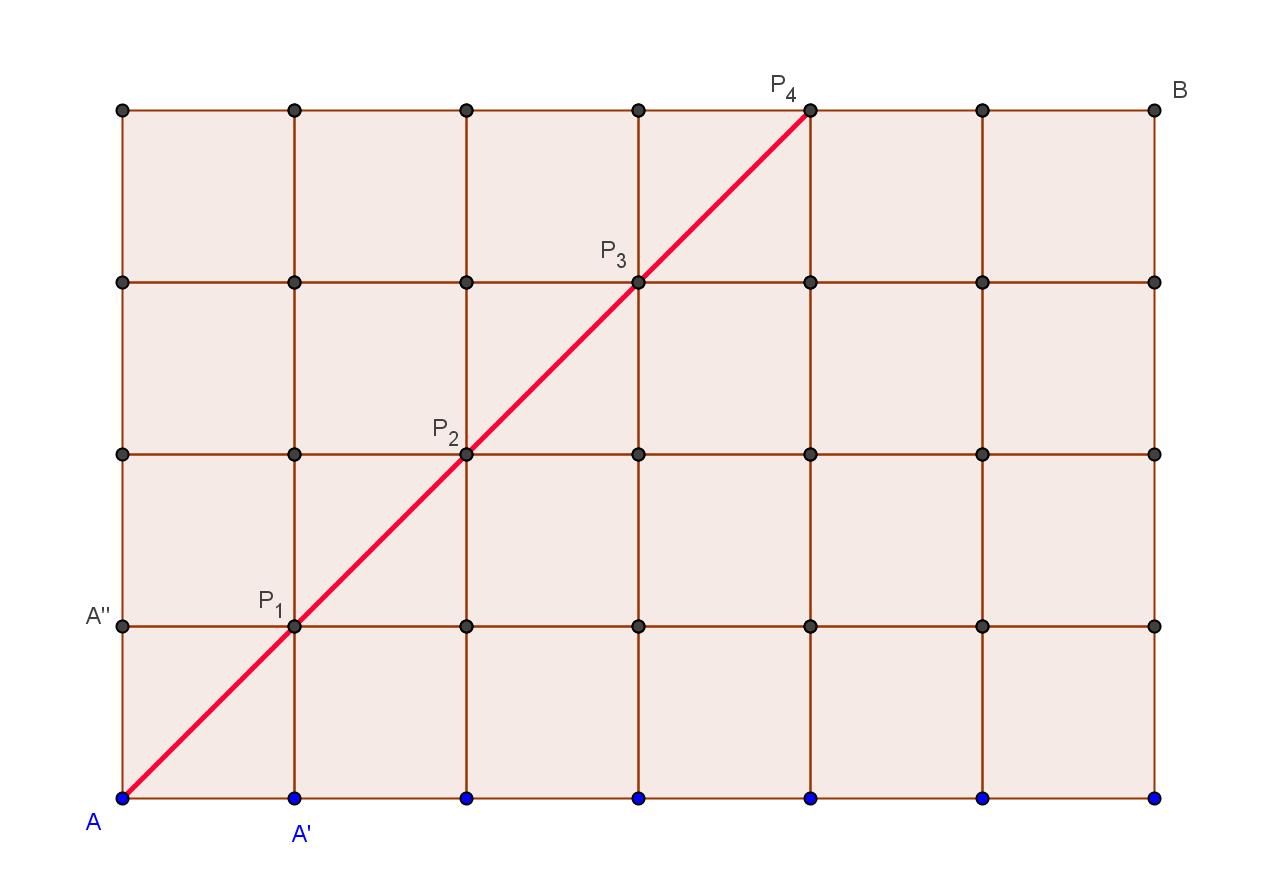
如圖,A走捷徑到B但是不能碰到\({{P}_{k}},k=1,2,3,4\),
觀察\(A'\to {{P}_{k}}\to B\) 的不合走法數由於對稱的關係會等於\(A''\to {{P}_{k}}\to B\) 的不合走法數,
每1種不合走法會一一對應,又\(A''\to B\)的每一種走法均為不合,故所求機率為
\(\frac{n\left( A'\to B \right)-n\left( A''\to B \right)}{n\left( A\to B \right)}=\frac{C_{5}^{9}-C_{6}^{9}}{C_{6}^{10}}=\frac{6-4}{6+4}=\frac{1}{5}\)
(推論:若size為向右m步,向上n步, \(m\ge n\) , 則所求機率為\(\frac{C_{m-1}^{(m-1)+n}-C_{m}^{m+\left( n-1 \right)}}{C_{m}^{m+n}}=\frac{m-n}{m+n}\) )
[ 本帖最後由 hua0127 於 2014-6-16 11:53 PM 編輯 ]
附件
-
 1.jpg
(54.43 KB)
1.jpg
(54.43 KB)
-
2014-6-16 17:57