單選3
(1)
\( \Bigg[\; \matrix{x^{''} \cr y^{''}} \Bigg]\;=\Bigg[\; \matrix{cos 2 \alpha & sin 2 \alpha \cr sin 2 \alpha & -cos 2 \alpha} \Bigg]\; \Bigg[\; \matrix{cos 80^{\circ} & -sin 80^{\circ} \cr sin 80^{\circ} & cos 80^{\circ}} \Bigg]\; \Bigg[\; \matrix{x \cr y} \Bigg]\; \)
點旋轉矩陣\( \Bigg[\; \matrix{cos \theta & -sin \theta \cr sin \theta & cos \theta} \Bigg]\; \)

鏡射\( \Bigg[\; \matrix{cos 2 \theta & sin 2 \theta \cr sin 2 \theta & -cos 2 \theta} \Bigg]\; \)

(2)L:\( (\sqrt{3}-1)x-(\sqrt{3}+1)y=0 \) \( m=2-\sqrt{3} \)
\( \sqrt{1^2+(2-\sqrt{3})^2}=\sqrt{8-2 \sqrt{12}}=\sqrt{6}-\sqrt{2} \)
\( \displaystyle cos \alpha=\frac{1}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{6}+\sqrt{2}}{4}=sin 75^{\circ} \)
\( \alpha=15^{\circ} \)或\( \alpha=-15^{\circ} \)

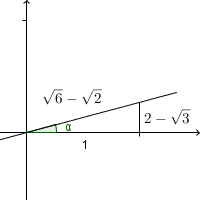
(3)\( y=(tan \theta )x \)
\( m=tan \theta \),\( \theta \)斜角
鏡射\( \Bigg[\; \matrix{cos 2 \theta & sin 2 \theta \cr sin 2 \theta & -cos 2 \theta} \Bigg]\; \)

(4)
\( \Bigg[\; \matrix{cos 2 \alpha & sin 2 \alpha \cr sin 2 \alpha & -cos 2 \alpha} \Bigg]\; \Bigg[\; \matrix{cos 80^{\circ} & -sin 80^{\circ} \cr sin 80^{\circ} & cos 80^{\circ} } \Bigg]\; =\Bigg[\; \matrix{cos 2 \theta & sin 2 \theta \cr sin 2 \theta & -cos 2 \theta} \Bigg]\; \)
\( cos 2 \alpha cos 80^{\circ}+sin 2 \alpha sin 80^{\circ}=cos 2 \theta \)
\( cos(2 \alpha-80^{\circ})=cos 2 \theta \)
\( 0<2 \theta <360^{\circ} \)
\( \alpha=15^{\circ} \)
\( 2 \alpha-80^{\circ}=-50^{\circ} \)
\( -50^{\circ}+360^{\circ}=310^{\circ} \)
\( 2\theta=310^{\circ} \)
\( \theta=155^{\circ} \)
單選4 把圖畫出來,就可以看出答案
[
本帖最後由 shingjay176 於 2014-6-4 12:59 PM 編輯 ]