填充 10.(前提假設斜面和底面夾 \( 45^\circ \) ) 暴力積分 \( \int_{0}^{1}\int_{0}^{x}2\sqrt{1-x^{2}}dzdx=2\int_{0}^{1}x\sqrt{1-x^{2}}dx=\left.2(1-x^{2})^{\frac{3}{2}}\cdot\frac{2}{3}\cdot(-\frac{1}{2})\right|_{0}^{1}=\frac{2}{3} \)

半徑 6，故所求 \( =6^3 \times \frac23 = 144 \) (好像也算錯了？)

如果是 #9 superlori 所言的 \( 30^\circ \)，那就沒錯了 \( 144 \tan 30^\circ = 48 \sqrt{3} \)

計算1.1 另證：

由 O 對直線 \( \overleftrightarrow{BC} \) 作垂線 \( \overline{OH_A} \) 垂直 \( \overleftrightarrow{BC} \) 於 \( H_A \)

\( \overline{OH} \perp ABC面 \), \( \overline{OH_A} \perp \overleftrightarrow{BC} \) 由三垂線定理得 \( \overline{HH_A} \perp \overleftrightarrow{BC} \)

\( \overline{AO} \perp OBC面 \), \( \overline{OH_A} \perp \overleftrightarrow{BC} \) 由三垂線定理得 \( \overline{AH_A} \perp \overleftrightarrow{BC} \)

故 \( A, H, H_A \) 三點共線，都在平面 OBC 上的過 H_A 垂直 \( \overleftrightarrow{BC} \) 的直線上

因此高 \( \overline{AH_A} \) 通過 H，同理另兩高亦過 H，三高交於 H，H即為垂心

第2小題 \( \displaystyle \frac{1}{6}abc = \frac{\sqrt{a^2b^2+b^2c^2+c^2a^2}}{2} \times \frac{h}{3} \)，其中 \( \frac12 \sqrt{a^2b^2+b^2c^2+c^2a^2} \) 為 \( \triangle ABC \) 的面積
(感謝 #73 mandy 指正 \( \triangle ABC \) 的面積)

整理即得 \( \displaystyle \frac{1}{h^2} = \frac1{a^2} + \frac1{b^2} + \frac1{c^2} \)

[ 本帖最後由 tsusy 於 2014-7-19 09:07 AM 編輯 ]

計算 6. 用 ggb 畫圖，四點共圓，需要條件是 \( \displaystyle \frac{\overline{CE}}{\overline{DE}} = \frac{\overline{CF}}{\overline{BC}} \)

計算 5. 有點看不太懂題目，沒有說明的對應關係應該是指這樣吧？

4 樓 4 扇 A  B  C  D
3 樓 3 扇   E  F  G
2 樓 2 扇     H  I

倒三角的對應關係，AB→E, BC→F, CD→FG, EF→H, FG→I

計算 5. 如原題意，如先前之猜測

我們以 0 表是打開， 1 表示關閉，則上下樓層的開關對應關係即模 2 的加法運算

例：開  開  關  開     0  0  1  0
          開   關  關         0  1  1

以 \( a_i \equiv 0 \) 或 1 (mod 2), \( i =0,1,2,3,\ldots,1023 \) 表示 \( 2^{10} \) 層的窗戶開關態，
依題意其中有 \( 2^9 + 1 \) 個 \( a_i \) 為  0； \( 2^9 - 1 \) 個 \( a_i = 1 \)

觀察此倒三角形加法關係 \( a_i \) 的係數，不難發現是二項式係數

故 1 樓的狀態為 \( \displaystyle \sum_{i=0}^{1023} C^{1023}_{i} a_i \)

接著我們需要一個小性質 \( C^{1023}_{i} \equiv 1 \) (mod 2)，這件事可以 Lucas 定理得到

Lucas 定理：若 \( p \) 為質數，\( m = a_0 + a_1 p +a_2 p^2 +\ldots \), \( n = b_0 + b_1 p +b_2 p^2 + \ldots \) 為兩非負整數滿足 \( 0 \leq n \leq m \) 且 \( 0\leq a_i, b_i < p \) 則 \( C^m_n \equiv \displaystyle \prod C^{a_i}_{b_i} \) (mod \( p \))
(即 \( a_i, b_i \) 為 \( n, m \) 的 \( p \) 進位表示式的各個位數)

所以 1 樓的狀態為 \( \displaystyle \sum_{i=0}^{1023} C^{1023}_{i} a_i \equiv 2^9 -1 \equiv 1 \) (mod 2)，即該窗戶關閉

[ 本帖最後由 tsusy 於 2014-6-1 09:05 AM 編輯 ]

身為去年過來人，我也來說說：

對不認識的老師來說，這樣的假考，他們可能無從得知。

但總有認識的老師正在努力通過教甄，這樣的假考，他們做何感想？或許一兩次無感？或許沒有說出口？

但這樣的行為，大概很難說自己問心無愧吧？

然後去年我去考了，對自己說我是去記題目的，順帶測測自己的水平有沒有下降。

但還是希望盡量不要影響到認真考試的老師們，

於是思量後挑一間，題目難、報名人數少 1 / 77、通過初試 6(實際) / 8(簡章)、說不定複試會從缺。

結果來看是既背了題目，又沒佔到真正的位子。當然事情可一不可再，再考下去的話，大概認識的會想揍我吧！

另外也可以效法老王老師，寫一個小時交卷，或是把剩下的時間拿來背題、抄題。

計算 6(1)

硬是寫一個爛證明，畫圖觀察，先想像 \( \angle DGC = 120^\circ \)，如果要用相似三角形證明此，會是哪個三角形與其相似呢？找到之後，再來湊相似條件

2014.06.03.103武陵高中.png (20.49 KB)

2014-6-4 00:00

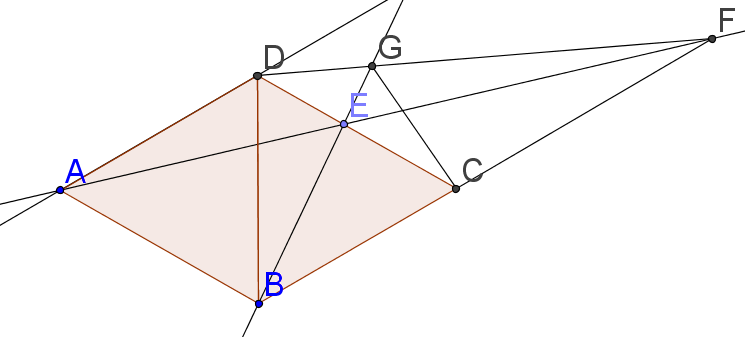
不妨假設 \( \overline{DE}=1, \overline{EC}=r \), 則 \( \overline{BC}=\overline{CD}=\overline{DA}=1+r \)。

由三角形 \( \triangle ADE\sim\triangle FCE \)，可得 \( \overline{CF}=(1+r)r \)

\( \triangle FDC \) 中，由餘弦定理可得 \( \overline{DF}=\sqrt{(1+r)^{2}+(1+r)^{2}r^{2}+r(1+r)^{2}}=(1+r)\sqrt{1+r+r^{2}} \)。

\( \triangle FDC \) 被直線 \( \overrightarrow{BE} \) 所截，由孟氏定理有 \( \displaystyle \frac{\overline{FG}} {\overline{GD}}\cdot\frac{\overline{DE}}{\overline{EC}}\cdot\frac{\overline{CB}}{\overline{BF}}=1
  \Rightarrow\frac{\overline{FG}}{\overline{GD}}=r(r+1)\Rightarrow\overline{DG}=\frac{1}{r^{2}+r+1}\overline{DF}=\frac{1+r}{\sqrt{r^{2}+r+1}} \)

\( \displaystyle \frac{\overline{DG}}{\overline{DC}}=\frac{1}{\sqrt{r^{2}+r+1}}, \frac{\overline{DC}}{\overline{DF}}=\frac{1}{\sqrt{1+r+r^{2}}} \)，又 \( \triangle CDG \) 和 \( \triangle FDC \) 共用 \( \angle D \)，故兩三角形相似(SAS)

因此 \( \angle DGC=\angle DCF=120^{\circ} \)，故 \( \angle DGC \) 與 \( \angle DBC \) 互補，因此四點共圓。

要是真的這樣做的話，考試根本做不出來吧。至於有沒有好方法，就請其它高手出手吧！

[ 本帖最後由 tsusy 於 2014-6-4 12:00 AM 編輯 ]

計算6(2)，補一下過程，由 (1) 得 BDGC 四點共圓，得 \( \angle BDG + \angle GCB = 180^\circ \)，故鋼琴兄 #39 的圖中將 \( \triangle BDG \) 以 \( B \) 為中心，逆時針旋轉 \( 60^\circ \) 得 \( \triangle BD'G' \)，其中 \( D' \) 和 \( C \) 重合。

由  \( \angle BDG + \angle GCB = 180^\circ \) 得 \( \angle BD'G' + \angle GCB = 180^\circ \)，故 \( GCG' \) 三點共線

四邊形 BDGC 面積 = 三角形 BDG 面積 + 三角形 BGC 面積
                               = 三角形 BD'G' 面積 + 三角形 BGC 面積
                               = 三角形 BGG' 面積 (邊長為 \( a \) 的正三角形)

你寫的才對，是我先前寫錯了，

至於 \( \triangle ABC \) 的面積，可用畢氏定理的推廣得到，推廣可見於  畢氏定理的兩個推廣-蔡聰明 第一頁下方處

而得 \( \triangle ABC = \frac12 \sqrt{a^2b^2+b^2c^2+c^2a^2} \)

一般來說，可能不特別定義 \( C^n_m \) 當 \( n <m \)

在這裡是，規定 \( n < m \) 時是將記號 \( C^n_m \) 當作 0, \( C^0_0 \) 當作 1

這樣在定理記號上的陳述會方便些。

如果要一個解釋的話，可以看作 \( (1+x)^0 = 1 + 0x  (C^0_0x^0+C^0_1x^1) \)，也就是說這樣定法跟二項式係數有某種一致性

另外，"個人"覺得 Locas 定理在考教甄裡，算是不太重要的定理，不太用得到

最原先，這題中，我的作法也不是用 Locas 定理，只是覺得證得有點麻煩，懶得打字，所以才用 Lucas 定理一句話帶過

[ 本帖最後由 tsusy 於 2014-8-26 09:33 PM 編輯 ]