3.
設空間中\( P(x,y,z) \)滿足不等式\( \displaystyle \Bigg\{\; \matrix{0 \le x+y \le 2 \cr 0 \le y+z \le 2 \cr 0 \le x+z \le 2} \),此P點之點集合形成一平行六面體,求此平行六面體體積為?
[解答]
\( x+y=0,y+z=0,z+x=0 \)這三個平面相交於原點\( O=(0,0,0) \)
平面\( x+y=0 \)和\( y+z=0 \)交線的方向向量為\( OA=(1,-1,1) \)
點\( A(1,-1,1) \)會落在平面\( z+x=2 \)上
平面\( y+z=0 \)和\( z+x=0 \)交線的方向向量為\( OB=(1,1,-1) \)
點\( B(1,1,-1) \)會落在平面\( x+y=2 \)上
平面\( z+x=0 \)和\( x+y=0 \)交線的方向向量為\( OC=(-1,1,1) \)
點\( C(-1,1,1) \)會落在平面\( y+z=2 \)上
此平行六面體體積為\( \displaystyle \Bigg\Vert\; \matrix{1 & -1 & 1 \cr 1 & 1 & -1 \cr -1 & 1 & 1} \Bigg\Vert\;=4 \)

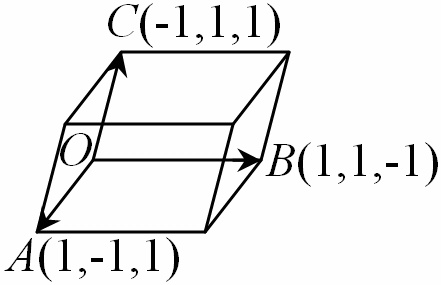
雖然看起來很像立方體,但實際上卻不是
你可以下載附件並開啟SketchUp觀察形狀
空間中 \(\left\{\begin{array}{ccc} 0&\le& x+2y &\le& 4\\ -1&\le& x-3y+z &\le& 3\\ 1&\le& x+3y-2z&\le& 7 \\ \end{array}\right.\)所圍成的平行六面體體積是多少?
(99文華高中,
https://math.pro/db/viewthread.php?tid=924&page=1#pid1993)