計算第 3 題：

思考：題目就是把 \(5^{100}\) 以二進位表示之後，此二進位表示法為 \(n+1\) 位數字，求 \(n\) 之值。

解題：

\(\displaystyle \log_2 5^{100}=100\log_2 5 = 100\cdot\frac{1-\log_{10} 2}{\log_{10} 2}\)

　　\(\displaystyle \approx 100\cdot \frac{1-0.3010}{0.3010}\approx 232.225\)

　　\(=232+0.225\)

　　\(=\log_2 2^{232} + \log_2 a\)　，其中 \(1<a<2\)

\(\Rightarrow 5^{100}=a\cdot 2^{232}\) （其中 \(1<a<2\)）

故，\(n=232\)

註： 依題意，可知 \(2^n\leq 5^{100}<2^{n+1}\)

填充第 5 題：

\(\displaystyle f(x)=\sin2x+2a\cos^2 x-a=\sin2x+2a\cdot\frac{1+\cos2x}{2}-a\)

　　\(\displaystyle =\sin2x+a\cos2x=\sqrt{1+a^2}\sin\left(2x+\theta\right)\)

其中 \(\displaystyle \sin\theta=\frac{a}{\sqrt{1+a^2}}, \cos\theta=\frac{1}{\sqrt{1+a^2}}\)

因為正弦函數 \(y=\sin x\) 的圖形對稱於 \(\displaystyle x=\frac{\pi}{2}+k\pi\) 其中 \(k\) 為任意整數

可知 \(f(x)\) 的圖形對稱於 \(\displaystyle x=\frac{1}{2}\left(\left(\frac{\pi}{2}+k\pi\right)-\theta\right)\)

依題意，

\(\displaystyle \Rightarrow \frac{-\pi}{8}=\frac{1}{2}\left(\left(\frac{\pi}{2}+k\pi\right)-\theta\right)\)，其中 \(k\) 為整數

\(\displaystyle \Rightarrow \theta=k\pi+\frac{3\pi}{4}\)

\(\displaystyle \Rightarrow a=\tan\theta=\tan\left(k\pi+\frac{3\pi}{4}\right)=-1\)

計算題第 2 題：
\(A(7,6,3)\)，\(B(5,-1,2)\)，\(L\)：\(\displaystyle \frac{x-1}{2}=y=\frac{z-3}{-2}\)，\(P\)為\(L\)上的動點，求使得\(\overline{PA}+\overline{PB}\)有最小值的\(P\)點坐標。
[解答]
令 \(P(1+2t, t, 3-2t)\)

則

\(\displaystyle \overline{PA}+\overline{PB}=\sqrt{\left(7-\left(1+2t\right)\right)^2+\left(6-t\right)^2+\left(3-\left(3-2t\right)\right)^2}+\sqrt{\left(5-\left(1+2t\right)\right)^2+\left(-1-t\right)^2+\left(2-\left(3-2t\right)\right)^2}\)

　　\(\displaystyle =\sqrt{9t^2-36t+72}+\sqrt{9t^2-18t+18}\)

　　\(\displaystyle =3\left(\sqrt{\left(t-2\right)^2+2^2}+\sqrt{\left(t-1\right)^2+1^2}\right)\)

令 \(Q(t,0),A(2,2),B(1,-1)\)

則 \(\displaystyle \overline{QA}+\overline{QB}=\sqrt{\left(t-2\right)^2+2^2}+\sqrt{\left(t-1\right)^2+1^2}\)

可知當 \(Q,A,B\) 共線時，\(\overline{QA}+\overline{QB}\) 有最小值，

此時 \(\displaystyle t=\frac{4}{3}\)

即當 \(\displaystyle P(\frac{11}{3}, \frac{4}{3}, \frac{1}{3})\) 時，\(\overline{PA}+\overline{PB}\) 會有最小值。

填充第 2 題：
若不等式\(5x^2-log_a x<0\)在\(\displaystyle x \in \frac{1}{5}\)內恆成立，則\(a\)的取值範例為　　　。
[解答]
當 \(a>1\) 時，因為 \(y=5x^2\) 通過原點且當 \(x\to0^+\)時，\(y=\log_a x\to -\infty\)

qq1.png (9.36 KB)

2013-7-17 23:06

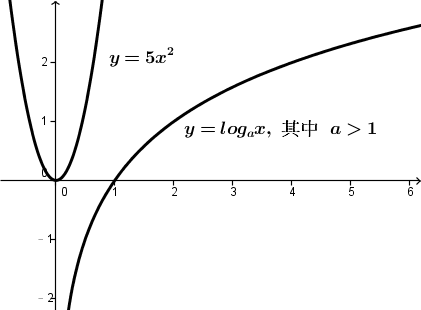
所以顯然 \(\displaystyle a>1\) 題述之不等式必然不成立。




當 \(0<a<b<1\) 時，因為 \(\displaystyle \log_a x<\log_b x, \forall 0<x<1\)

qq2.png (40.54 KB)

2013-7-17 23:15

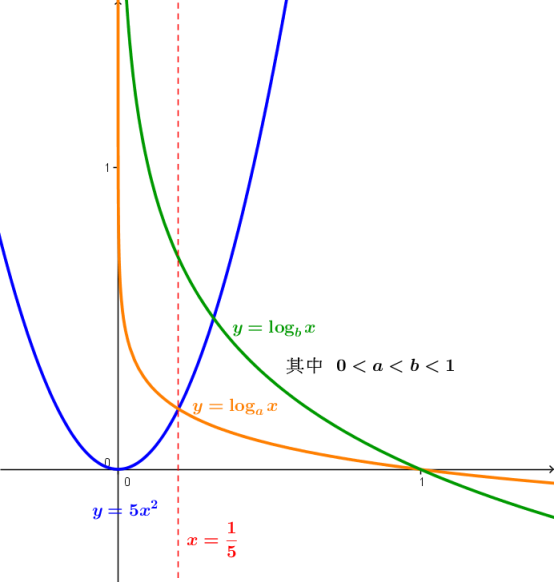
因此，只需要確認當 \(a\) 值為何時，會使得 \(y=5x^2\) 與 \(y=\log_a x\) 交點的 \(x\) 坐標是 \(\frac{1}{5}\)

\(\displaystyle\Rightarrow \log_a\left(\frac{1}{5}\right)=5\left(\frac{1}{5}\right)^2\)

\(\displaystyle \Rightarrow a^\frac{1}{5}=\frac{1}{5}\Rightarrow a=\frac{1}{5^5}=\frac{1}{3125}\)

即當 \(\displaystyle \frac{1}{3125}\leq a<1\) 時，恆有 \(\displaystyle 5x^2<\log_a x, \forall x\in\left(0,\frac{1}{5}\right)\)

你可以先看一下 https://math.pro/db/viewthread.php?tid=1652&page=3#pid8927 回覆的前半段就是了。（令\(u=2x\)）

填充第 1 題：
填充1.
設\(G\)為\(\Delta ABC\)的重心，直線\(L\)過\(G\)且分別交\(\overline{AB}\),\(\overline{BC}\)於\(M,N\)。若\( \vec{BM}=a \vec{BA} \)，\( \vec{BN}=b \vec{BC} \)(其中\(a>0\)，\(b>0\))，則\(ab\)的最小值為　　　。
[解答]
設 \(\overline{AC}\) 的中點為 \(D\)，

則 \(\displaystyle \vec{BG}=\frac{2}{3}\vec{BD}=\frac{2}{3}\left(\frac{1}{2}\vec{BA}+\frac{1}{2}\vec{BC}\right)=\frac{1}{3}\vec{BA}+\frac{1}{3}\vec{BC}=\frac{1}{3a}\vec{BM}+\frac{1}{3a}\vec{BN}\)

因為 \(G,M,N\) 共線，所以 \(\displaystyle \frac{1}{3a}+\frac{1}{3b}=1\)

由算幾不等式，可知 \(\displaystyle \frac{\displaystyle \frac{1}{3a}+\frac{1}{3b}}{2}\geq\sqrt{\frac{1}{3a}\cdot\frac{1}{3b}}\Leftrightarrow ab\geq\frac{4}{9}\)

且當 "\(=\)" 成立時， \(\displaystyle a=b=\frac{2}{3}\)

因此，\(ab\) 的最小值為 \(\displaystyle\frac{4}{9}.\)

是非題第 2 題：

有「可能」，

例如，若給的點是「短軸上一頂點及兩焦點」，則可以算出半長軸長，

然後再按照定義求出橢圓方程式。

是非題第 3 題：

因為 \(\left|2x-3\right|+\left|x-5\right|\geq\left|\left(2x-3\right)-\left(x-5\right)\right|\) 恆成立，

且等號成立時，\(\left(2x-3\right)\left(x-5\right)\leq0\)

題目說 \(\left|2x-3\right|+\left|x-5\right|\leq\left|x+2\right|\) ，

搭配 \(\left|2x-3\right|+\left|x-5\right|\geq\left|x+2\right|\) 恆成立，

就是 \(\left|2x-3\right|+\left|x-5\right|=\left|x+2\right|\)

因此 \(\left(2x-3\right)\left(x-5\right)\leq0.\)