有鑑於學校沒公告數學科的試題

所以來回憶一下題目，有的地方沒有記得很清楚

還請有考試的考生幫忙回憶一下，謝謝！部分題目可能不太正確

其中填5 的圖是自己畫的，跟試卷的標記可能不太一樣，也忘了要求哪段的長度了

填10，則是只記得形狀，忘記數字了，經 Google 大神協助本題出處應為 2004年(第三屆)中國女子數學奧林匹克試題
數字為 \( \frac{a+3c}{a+2b+c}+\frac{4b}{a+b+2c}-\frac{8c}{a+b+3c} \)

填11，敘述也許和原題有出入?因為題目寫得太長了

另外填12，題目是否有給 \( x> -1 \) 之類的條件？

請慢慢享用

附上部分個人算的數字，僅供參考，歡迎指正。

填充題
1. \( -\frac{159}{160} \)                     2. \( \frac{5}{2} < b < 4 \)

3. \( \frac{1}{32} \)                         4. 2084

5. \( \frac{1+\sqrt{4\sqrt{3}-3}}{2} \)          6. \( \frac{6}{11} \)

7. \( \frac{1}{\sqrt{10}} \)                      8. \( \frac{4}{5} \)

9. \( x< \frac{1-\sqrt{5}}{2} \) 或 \( 1 < x < \frac{1+\sqrt{5}}{2} \)

10. \( -17+12\sqrt{2} \)       11.\( n-1 \)

12. \( \frac{1}{x+1} \)

計算3. \( (0,0,z) \) 及 \( (1,-1,-1) \)

附件檔案修正
2. 修正填 2 的敘述，感謝鋼琴大修正。
3. 補上漏掉的條件 \( f(\frac{x}{6}) = \frac{f(x)}{2} \)，感謝鋼琴大提醒。
5. 應該求 \( \overline{BE} \) 之長。
8. 修正為 \( bx^2 \)，感謝 dream10 提醒修正。
12. 修正為 \( t^x \)

請教填充 9,2 有無什麼好方法

9.
不等式\(\displaystyle \frac{2x^2-4x+3}{(x-1)^3}>x^3+2x\)的實數解為　　　　。
[解答]
個人的想法是 \( LHS = \frac{2}{x-1} + \frac{1}{(x-1)^3} \) 分段遞減。而且在 \( 1\pm \) 處為 \( \pm \infty \)

而 \( RHS = x^3+2x \) 微分可知，嚴格遞增。

故僅需解 \( \frac{2x^2-4x+3}{(x-1)^3} = x^3+2x \) 之兩實根。

即方程式 \( x^{6}-3x^{5}+5x^{4}-7x^{3}+4x^{2}+2x-3=0 \) 之兩實根 \( \alpha< \beta \)

而不等式之解則為 \( x < \alpha \vee 1 < x < \beta \)。

但易驗，該六次式沒有理根，然後就卡了

附上 Wolfram Alpha 的答案 \( x < \frac{1-\sqrt{5}}{2} \) 或 \( 1<x<\frac{1+\sqrt{5}}{2} \)

2.
平面上坐標上，\(\Gamma\)為所有的點\(P\)滿足到直線\(x=4\)與\((1,0)\)的距離和為5之曲線。試求\(b\)的範圍，使得\(\Gamma\)上恰有三組點，關於點\((b,0)\)對稱。
[解答]
想法，先畫個概圖

pic.png (11.03 KB)

2013-4-14 09:28

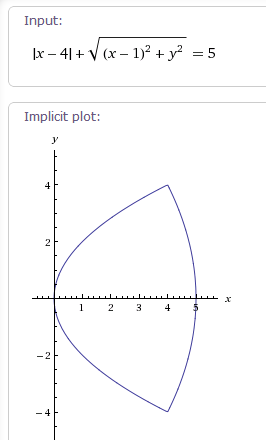
注意上下對稱於 x 軸 必一組，另兩組為是 \( y = \pm c \)，四個交點成矩形，畫個對角線交點就是 \( (b,0) \)

但 \( c=0 \), \( b =\frac52 \) 會多出一組左右對稱點，隨著 \( c \) 從 \( 0\to 4\)，猜測 \( b \) 從 \( \frac52 \to 4 \)

故猜答案為 \( \frac52 < b < 4 \)

解得漂亮，原來是把 2 跟 2 放一起，1 跟 1 也放一起

什麼時候我才可以也有這種眼力，看出其中竅門所在

原來如此~~感謝 Joy091 解惑

另外填 3 是個有趣的題目，做法如下

填 3.
若函數\(f(x)\)滿足\(f(1)=1\)，\(f(x)+f(1-x)=1\)，\(\displaystyle \frac{x}{6}=\frac{1}{2}f(x)\)，其中\(0\le x\le 1\)，且對\(0\le x_1<x_2\le 1\)，有\(f(x_1)\le f(x_2)\)，則\(\displaystyle f(\frac{1}{2013})=\)　　　。
[解答]
注意由函數之性質可得 \(f(\frac16) = \frac12 = f(\frac56) \)

又 \( \frac16 < \frac{6^4}{2013} < \frac56\), 故 \( f(\frac{6^4}{2013})=\frac12\)

因此所求 \( f(\frac1{2013}) = \frac1{32}\)

補充一類題：設函數 \(f (x) \) 在\( 1 \leq x\leq  3\) 時，滿足 \(f (x) =1-|x-2|\) ，且對所有的正數 \(x\)，\(f (x)\) 滿足\(f(3x) = 3f (x)\)。試求最小的正數 \(x\) 使得 \(f (x) = f (2011)\)。
(100二區能力競賽 )(2001AIME 則是 2011變成 2001)

填 4.
\(\displaystyle \sum_{k=1}^{2013}\Bigg[\;\root 5 \of {\frac{2013}{k}} \Bigg]\;=\)　　　。([]為高斯符號)
[解答]
則是基本的題型，提供一個有趣的方法：Fubini 定理

令 \( S=\{\sqrt[5]{\frac{2013}{k}}\mid k=1,2,3\ldots,2013\} \), \( S_{n}=S\cap\{x\mid x\geq n\} \)。

由 Fubini 定理有 \(\sum\limits _{k=1}^{2013}\left[\sqrt[5]{\frac{2013}{k}}\right]=\sum\limits _{n=1}^{\infty}|S_{n}|\) 。

\( \left[\sqrt[5]{\frac{2013}{k}}\right]\geq n\Leftrightarrow\frac{2013}{k}\geq n^{5}\Leftrightarrow\frac{2013}{n^{5}}\geq k \)，

故 \( |S_{n}|=\left[\frac{2013}{n^{5}}\right]=2013,62,8,1,0,0\ldots \)。故所求 \(=2013+62+8+1=2084\)。

類題：2. \(y=[x] \) 表高斯函數，求 \(\sum\limits _{k=1}^{40}\left[10^{\frac{k}{40}}\right]\)。(101文華高中)

1.
設\(f(x)\)為一317次多項式滿足\(\displaystyle f(k)=\frac{1}{k}\)，\(k=1,2,3,\ldots,318\)，則\(f(320)=\)　　　。
[解答]
要直接用插值多項式做，也不是不可以，只是組合恆等式要熟一點，可以像下面這樣做

以拉格朗日，插值多項式表示之，令 \( f(x)=\sum\frac{1}{k}f_{k}(x) \)，其中 \( f_{k}=\frac{\prod_{i=1}^{k-1}(x-i)\cdot\prod_{i=k+1}^{318}(x-i)}{\prod_{i=1}^{k-1}(k-i)\cdot\prod_{i=k+1}^{318}(k-i)}=(-1)^{k}\frac{\prod_{i=1}^{k-1}(x-i)\cdot\prod_{i=k+1}^{318}(x-i)}{(k-1)!(318-k)!} \)

而 \( \frac{1}{k}f_{k}(320)=\frac{(-1)^{k}}{k}\cdot\frac{319!}{320-k}\cdot\frac{1}{(k-1)!(318-k)!}=(-1)^{k}\frac{319-k}{320}\frac{320!}{k!(320-k)!}=(-1)^{k}\frac{319-k}{320}C_{k}^{320} \)。

注意 \( (1+x)^{320}=\sum\limits _{k=0}^{320}C_{k}^{320}x^{k} \)，微分得 \( 320(1+x)^{319}=\sum\limits _{k=1}^{320}kC_{k}^{320}x^{k-1} \)。

將 \( x=-1 \) 代入得 \( \sum\limits _{k=0}^{320}(-1)^{k}C_{k}^{320}=0 \), \( \sum\limits _{k=1}^{320}(-1)^{k-1}kC_{k}^{320}=0 \)。

故所求
\( \begin{aligned}f(320) & =\sum\limits _{k=1}^{318}\frac{1}{k}f_{k}(x)=\frac{319}{320}\cdot\sum\limits _{k=1}^{318}(-1)^{k}C_{k}^{320}+\frac{1}{320}\cdot\sum\limits _{k=1}^{318}(-1)^{k-1}kC_{k}^{320}\\
& =\frac{319}{320}\cdot(-1+320-1)+\frac{1}{320}\cdot(320-319\cdot320)\\
& =-\frac{159}{160}
\end{aligned} \)

做樣，挺累的...而且一不小心就會出錯，所以還是看樓上連結裡的方法吧

填 5. 再補另一個解法：

102Jianguo5.png (26.03 KB)

2013-4-16 20:44

由面積可知正方形之邊長為 \( \sqrt[4]{3} \)。注意直角的位置，可知正方形左下角為原來的 \( H \)，右上角為原來的 \( I \)。

並且正方形之一邊(最右邊)為 \( 2\overline{GI}=\sqrt[4]{3} \) \( \Rightarrow\overline{GI}=\frac{\sqrt[4]{3}}{2} \)。坐標化，

令 \( G(0,0), F(-1,0), B(-\frac{3}{2},-\frac{\sqrt{3}}{2}) \), \( r=\frac{\sqrt[4]{3}}{2} \)。

再令 \( \Gamma \)  為一圓，其圓心為 \( G \)，半徑為 \( r \)，則 \( \overline{FE} \) 為圓 \( \Gamma \) 之切線。

計算此切線方程式得 \( y=-\sqrt{\frac{\sqrt{3}}{4-\sqrt{3}}}(x+1) \)，其與 \( y=-\frac{\sqrt{3}}{2} \) 之交點 \( E \)  之坐標為 \( (\frac{\sqrt{4\sqrt{3}-3}}{2}-1,-\frac{\sqrt{3}}{2}) \)。

故所求 \( \overline{BE}=\frac{\sqrt{4\sqrt{3}-3}}{2}-1+\frac{3}{2}=\frac{1+\sqrt{4\sqrt{3}-3}}{2} \) 。

填 8.
若\(x^4+ax^3+bx^2+ax+1=0\)有實數解，則\(a^2+b^2\)的最小值為　　　。
[提示]
那樣係數首尾對稱的式子

常用 \(\displaystyle t = x+\frac1x \) 代換處理之

這樣就可以降低成二次方程式

抱歉，是我的手誤打錯了，是 \( t^x \) 才正確，已修正之。

這題，可以是初微的積分技巧，也可以是高微以上(上至實分析) 裡，微分和積分可否交換順序的層次

倒不是筆誤，而是寸絲記的題目就是那樣。

或許是記錯了吧？難怪一直做不出來

猜測，正確的命題應為 AP(BC-DE) >= BD PE + CE PD

不知道有沒有哪位，記得正確的題目，可以幫忙確認一下，謝謝！

填 7.
\(OABC\)為一邊長為1的正四面體，\(D,E\)分別為\(\overline{AB},\overline{OC}\)中點。兩歪斜線\(\overline{OD}\)和\(\overline{BE}\)的距離為　　　。
[提示]
坐標化 \(\displaystyle O(0,0,0), A(0,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}), B(\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}}), C(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0)\)，剩下的應該不難了。

填 12.
設\(\displaystyle F(x)=\int_0^1 \frac{t^x-1}{lnt}dt\)，則\(\displaystyle \frac{d}{dx}F(x)=\)　　　。
[解答]
若 \( x>-1 \)，則 \(\displaystyle t^{x}-1=\ln t\int_{0}^{x}t^{s}ds \), for \( t>0 \)

\(\displaystyle \Rightarrow F(x)=\int_{0}^{1}\int_{0}^{x}t^{s}dsdt=\int_{0}^{x}\int_{0}^{1}t^{s}dtds=\int_{0}^{x}\frac{1}{s+1}ds=\ln(x+1) \)。

故 \(\displaystyle \frac{d}{dx}F(x)=\frac{1}{x+1} \) 。